Artificial neural networks in the cancer genomics frontier

Introduction

Genomics is a branch of molecular biology concerned with the structure, function, and evolution of genomes, that is, of an organism’s hereditary information encoded in DNA. Cancer genomics is a subfield of genomics that deals with the application of high-throughput technologies used to identify genes associated with the development and progression of cancer. It is known that both, abnormalities in an individual’s germline genome, as well as somatic mutations play a role in cancer morbidity and mortality (1). To date, investigations in cancer genomics have resulted in the identification of roughly 140 genes, which may facilitate, or “drive”, tumorigenesis as a consequence of their intragenic mutations. Mutations in these cancer “driver” genes serve to increase the “cell birth to cell death” ratio, thereby conferring a selective growth advantage to the cell in which these genetic alterations take place (2).

The advent of DNA-microarray technology in the 1990s allowed researchers to simultaneously measure the expression levels of thousands of genes (3,4). This advance enabled scientist to (I) compare the genomes of tumors and healthy tissues, facilitating discovery and understanding of biological pathways involved in cell fate determination, cell survival, and genome maintenance (5-7); (II) improve diagnostic accuracy of tumor subtypes in cases where histological diagnosis is ambiguous (8-10); (III) monitor expression patterns over time to improve staging and risk assessment (11-13); and (IV) develop a deeper understanding of the tumor’s response to various therapeutics (14-16). Consequently, information gained form cancer genome studies may aid oncologists in the development of patient management plans that is guided by knowledge of an individual’s germline genome as well as the genome of the patient’s tumor (2).

Results from genomic research have already been translated to clinical implementation. In diagnostic applications, expression levels of 7 genes (PML-RARA, BCR-LBL1, CBFB-MYH11, ETV6-RUNX1, MLL-rearranged, TCF3-PBX1, RBM15-MKL1) are used for WHO classification of leukemia subtypes, while 13 different genes have been clinically implemented to differentiate between various types of sarcomas. In prognostic applications, Oncotype Dx (a 21-gene signature) and Mammaprint (a 71-gene signature) are being used to distinguish risk subgroups. Also, mutations in the BRAF, TP53, and FLT3-ITD genes are being used to identify prognostic subgroups for colorectal cancer (CRC), lymphocytic leukemia, and myeloid leukemia, respectively. Among genes that have been identified as predictive of therapeutic response are the EGFR, KIT, KRAS, BRAF, and HER2, corresponding to non-small-cell lung cancer, gastrointestinal stromal tumors, metastatic CRC, melanoma, and breast cancer, respectively (17). A famous example of germline mutations in tumor suppressor genes, BRCA1 and BRCA2 have been linked to a number of cancers, including breast and ovarian cancers (18).

The goal of this paper is to introduce the reader to artificial neural networks (ANNs) as they are used in cancer genomic studies, while providing a brief description of the components that comprise the analysis of genomic data. The rest of the paper is structured as follows: first, an introduction to the data and the issues that arise in its analysis; second, neural networks are described with the intent of providing a novice reader with information sufficient for understanding the processes that go on behind the scenes of a neural network implementation package in the performance of a basic classification task; third, a brief overview of pre-filtering and “gene-signature” selection methods is given; finally, a few notable applications are described in terms of the information given in parts 2 and 3. Also, a description of an illustrative example by the authors is provided at the end of the applications section.

Microarray technology and data collection

Due to its well-developed infrastructure, general acceptance, and relatively low cost, microarray experiments continue to be the most common source of data for cancer genomic studies (19). In microarray experiments, thousands of DNA sequences are arranged in probes and are exhibited in a high density array positioned on a microscope slide. Messenger RNA (mRNA) from both the tumor and the reference tissue are placed into the probes, where the mRNA of each tissue will bind to its complementary DNA (cDNA) in a process called hybridization. The data used for analysis is derived from the comparison of target gene expression across samples, which is accomplished by measuring the differential hybridization intensity of the sampled mRNA as it is reverse transcribed into the cDNA. In a two channel experiment, the two samples being compared are labeled with florescent dyes [usually Cy5 (red) for tumor and Cy3 (green) for the reference], and the hybridization of the samples with the arrayed DNA probes is measured by comparing fluorescence measurements of each dye. The relative gene expression between the tumor and reference samples is usually assessed as the log ratio of the two dye intensities (i,e.,Expression=log2RedGreen), where Red represents the dye intensity of the tumor, and Green represents that of the reference sample (20). One channel experiments are similar in nature, but involve hybridization of just one sample after it has been labeled with the dye (21). Other sources of genomic data stem from three generations of sequencing technologies that utilize a variety of techniques to amplify and compare expression of target DNA sequences. The reader is referred to (22) for a comprehensive review.

Issues with data analysis

Data analysis usually involves the extraction of patterns that can be useful for classifying a given tissue sample based on its gene expression profile. This procedure consists of identifying the genes that contribute most to successful classification, thereby deriving what is commonly termed a “gene-signature” (23). The class of interest may represent a diagnostic category (e.g., malignant or benign), a survival group based on the outlook without treatment (e.g., survival of 5 years or more, or not), or categories of treatment response (e.g., toxicity response to treatment with an EGFR kinase inhibitor).

Whether the data is generated in microarray experiments or from studies utilizing sequencing technologies, similar issues arise during analysis (24). One of the main issues is due to the high dimensionality of the data, which results from the fact that expression levels are measured simultaneously for thousands of genes in each tissue sample, where the number of samples usually differs from the number of measured genes by a couple of orders of magnitude (e.g., 3,000 genes per sample, measured for 80 samples) (25). Classifiers trained on highly dimensional data tend to fit the training data well, but when presented with a new set of gene features, as in clinical implementation, the classifier fails to correctly categorize the sample. This phenomenon of “overfitting” the data occurs when the classifier has learned to identify random, non-informative features that are peculiar to the particular dataset, instead of learning more general, high level features that are pertinent to the classification task at hand.

Numerous statistical/machine learning methods have been proposed for the analysis task in cancer genomics, including classification trees (26,27), naïve-Bayes classifiers (28,29), and support vector machines (30,31). ANNs have been successfully utilized for both, sample classification, as well as identification of diagnostic, prognostic, and predictive gene-signatures. Among the reasons for the ANNs’ success is their ability to process many noisy, correlated inputs, while utilizing their parallel nature for the simultaneous detection of a multitude of subtle features in the data. Further, an abundance of methods has been developed for finding the proper balance between model complexity, relevant feature extraction, and the modeling of non-linear discriminant boundaries necessary for the classification of genomic data.

Artificial neural networks (ANNs)

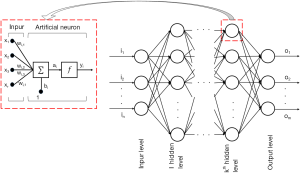
ANNs represent a class of computational models that are inspired by biological function of the human brain. ANNs are usually represented by a weighted, directed graph connecting inputs to a series of interconnected “hidden” layers that are comprised of multiple nodes called “neurons,” that are in turn connected to an output layer. The output nodes produce the desired approximations, often in terms of the conditional probability of class membership, given a particular input vector. The structure of each node in the “hidden” layer can be understood as a mathematical representation of a neuron, first suggested in the early works by McCulloch, Pitts, and Hebb (32). When this “neuron” receives stimuli from its connections to the preceding layer, it becomes activated and outputs a value, which is determined by a smooth activation function (e.g., sigmoid or tanh). The argument for the activation function is a weighted average of inputs produced by nodes from the preceding layer that are connected to this particular neuron by weighted connections. The weight that is associated with each directed connection represents the importance of the connection, while the directions establish the flow of information through the network. This pattern of interconnections is referred to as network architecture (33). Development of network architectures has been largely inspired by the connections among neurons in functional areas of the human brain, where the nodes in the ANN correspond to neurons that are stimulated by inputs at the dendrites (i.e., the weighted connections), that produce a single output at the axon, which in turn, is connected to other neurons at the next synaptic junction, and so on (34). When the architecture does not contain loops, the network is said to be a feed-forward network, also called the multilayer perceptron (MLP). The MLP is the architecture most often used in cancer genomic studies.

A graphical representation of a typical feed-forward multi-layer perceptron, for a multi-class/softmax classification problem, is depicted in Figure 1, and a mathematical representation of a single neuron can be formulated as:

Outputi=f(Wixi+b)[1]

Figure 1 Graphical representation of a feed-forward multi-layer perceptron, with a softmax classification output layer.

where f(x)=11+e−(x) is the sigmoid transfer function, xi is the ith input vector, Wi is the vector of connection weights for the ith</input and b is the bias term associated with a particular layer of inputs. Another common choice of a smooth transfer function is the hyperbolic tangent, f(x)=ex−e−xex+e−x.

Learning

It has been theorized that learning in the human brain, takes place by updating relationships between neurons, which is accomplished by changing the intensities of their connections, the synapses, such that the effect of one neuron’s activation on another neuron is no longer the same (35). In the ANN the synapse is modeled by the weight assigned to the connection between two neurons. The MLP learns to accurately associate input features with particular outputs by updating weights assigned to the multitude of network connections, such that the error between the network output values and the target outputs is minimized. This process can be imagined as iteratively moving around separating hyper-planes, that form boundaries between sample categories in input space, until all of the training inputs are correctly separated/classified (i.e., network error is minimized).

Network error is often defined as the squared Euclidean distance between the network output and the target value, and can be stated as the following objective function:

J(W,b;x,y)=12‖hW,b(x)−y‖2[2]

where h_w,b(x) is the hypothesized network output as a function of the inputs, x, and y is the target/true value. The same error function can be stated in more detail as:

J(W,b)=12(∑i=1m‖hw,b(x(i))−y(i)‖2)+λ2∑l=1nl∑i=1sl∑j=1sl+1(wijl)2[3]

where m is the number of training samples, nl is the number of layers in the network, sl is the number of nodes in the lth layer, and sl+1 is the number of nodes to which each node in the lth layer is connected. In other words, network error is comprised of the sum of squared errors, summed overall output units and all training samples. The second term in Eq. [2] is the “weight decay,” and will be described later in the paper. Since the network output value is represented as a function of network weights, the error function can be minimized with respect to these weights. The most popular method for solving this optimization problem is via a method known as gradient descent.

Gradient descent is a weight updating rule that is based on the fact that for any multidimensional surface, the direction of greatest increase/ascent is determined by the gradient of the surface function with respect to the parameters that define the surface. Thus, moving in the direction opposite to the gradient implies movement in the direction of steepest descent. As the goal of the optimization problem is to find a configuration of the weights such that the error function is at a minimum (i.e., the bottom of the error surface), taking incremental steps in the direction of steepest descent should eventually bring us to this minimum. Thus, under gradient descent, the weights of the MLP are iteratively updated according to the following rule:

wij(l)=wij(l)−α∂∂wij(l)J(W,b)[4]

bi(l)=bj(l)−α∂∂bj(l)J(W,b)[5]

where

α∂∂wij(l)J(W,b)=1m∑i=1mJ(W,b,x(i),y(i))+λwijl[6]

and wijl is the connection weight between unit j in layer l and unit i in layer l+1</, and bil is the bias associated with unit i in layer l+1</.

Learning is accomplished via the back propagation algorithm (36). An intuitive understanding of this process can be developed as follows. After the network architecture has been determined, the connection weights between all neurons are randomly initialized (usually to some small value, normally distributed around zero). Next, given a training example consisting of an input vector and the corresponding classification for the ith</tissue sample, a forward pass through the network is performed, in which activation values at all neurons, including the outputs, are computed. The error between the network output and the target classification is computed, and propagated backwards to all neurons that participate in the production of the output. The goal is to obtain a measurement of classification error for which each node in the network is responsible (37). Computation of this error at the output node is straightforward, since the both the output and the target value are known, while the error at each node in the hidden layers is computed as a weighted average of the errors at nodes in the subsequent layer that use this particular node as an input.

Step size

The parameter alpha in Eqs. [3,4 is known as “step size” or “learning rate” for the gradient descent algorithm, since it indicates the amount by which the weights are updated during each iteration of the algorithm. If this parameter is too small, then the algorithm may take a long time to converge and is more likely to get trapped in a local minimum. However, if step size is too large, the minimum may be overlooked and the algorithm may oscillate and fail to converge. Other issues regarding smooth and efficient implementation of the algorithm can be dealt with by an inclusion of other tuning parameters such as momentum, that are described in more detail in (38,39).

Weight decay

Problematic model generalization is rooted in overfitting, which is usually associated with large numbers of model degrees of freedom (e.g., the connection weights), as the bias-variance trade-off becomes unbalanced in the variance direction (40). Thus, it is of benefit to implement a design in which irrelevant connections between model neurons are removed. This may be accomplished via “weight decay”. The addition of this term to the network objective function ensures that some of the connection weights are forced to zero, effectively getting rid of connections with small weights that could have been assigned as a result of random noise in the training sample rather than a recognition of a pattern that is characteristic of the phenomenon of interest. The proper number of neurons in the hidden layer (i.e., the architecture) as well as the best value for the weight decay parameter, λ in Eq. [2], is usually determined through a process of cross-validation.

Cross validation

Cross validation is a quality assessment strategy which entails division of the training data into k distinct subsets. The model is than trained on the k–1 subsets, and its performance is tested on the omitted subset (41). This procedure is repeated, by “holding out” each of the k subsets, in turn, using the k–1 subsets for training, and the k^th subset for validation. The prediction errors from k such cycles are averaged and used to compare ANN models with different architectures and various weight decay, step-size, and momentum settings. This procedure is commonly termed k–fold cross validation. Another form of cross validation is performed by removing a single sample from the training set, training the classifier in its absence, and then using the input values of this missing sample to predict its output. This procedure is repeated for each sample in the training set, and the prediction quality is measured as an average of errors for each of these individual samples. This type of cross-validation procedure is referred to as “leave-one-out” cross-validation (41).

Filtering and gene selection

Often before gene expression data is fed into a classifier such as the neural network, preprocessing or filtering is required, in order to identify the genes relevant for classification. Some of the genes in a data set resulting from microarray experiments may have gene expression values that are not meaningful and do not vary across classes. To fix this problem, genes that have a range outside some meaningful value are removed. For example (42), let gij be the gene expression level of gene i for training sample j, then gene i may be removed if

maxj(gij)−minj(gij)<somemeaninfulquantitye.g.,500[7]

maxj(gij)>somemeaninfulquantitye.g.,16,000[8]

|maxj(gij)minj(gij)|<somemeaninfulquantitye.g.,5[9]

After such genes are removed, the relevance of genes can be ranked via a variety of methods. The two main criteria for the selection of relevant genes have to do with signal strength and redundancy. Signal strength may be measured by the signal to noise ratio (SNR), where the signal represents inter-class expression differences, while the noise represents intra-class variation (42). Similarly, relevance ranking for individual genes can be carried out by obtaining P-values from standard statistical tests [e.g., t-test comparing the expression levels of a particular gene across tumor and normal tissue (43), or a Cox regression model comparing survival time across different levels of gene expression (44)]. Significance analysis of microarrays (SAM), a version of the t-test that is based on a tolerable false discovery rate (FDR), is a popular choice for gene selection (45). Gene redundancy may result from co-expressed genes which are expressed in similar quantities across classes (42). This redundancy can be measured by standard correlation measures between two individual genes, such as the Pearson correlation coefficient, and thus can be controlled by implementing methods that take this correlation into account (46).

The results of the neural network may also be used to identify the genes that are most relevant to the classification task. This is often referred to as the “wrapper” method, in which model results are used to identify relevant genes (42). For example, sensitivity analysis may be performed by numerically taking derivatives of the network outputs with respect to the inputs in order to identify the genes that cause the classification to change the most. This can also be accomplished by removing genes, one by one from the input vectors and examining the change in classification accuracy. One way to identify relevant genes, and to reduce redundancy at the same time, is through a “consecutive search” method, of which there are two main types (42). Forward search begins with an empty set of genes to be used as inputs for the prediction model, and then adds one gene at a time to the set of inputs, based on the predictive value that the gene contributes to the set. In contrast, backward search begins with all of the available genes as inputs, and then sequentially gets rid of genes, whose removal has the smallest negative impact on the overall prediction value of the set of inputs. An approach that identifies relevant genes as well as reduces the dimensionality of the input space, is principal component analysis (PCA). PCA can be performed, using singular value decomposition (SVD) on the high dimensional input space, and then principal component scores, corresponding to the first p principal components that represent some acceptable amount of the total variation in the gene expression data (e.g., 70%), are used as inputs into the model. For a complete treatment of feature selection methods, the reader is referred to (47).

Applications

Javed Khan and colleagues were among the first to apply the power of neural networks to the problem of cancer classification (48). In this application, the researchers developed a model for classifying small, round blue cell tumors (SRBCTs) of childhood cancer into four diagnostic categories, neuroblastoma (NB), rhabdomyosarcoma (RMS), non-Hodgkin lymphoma (NHL), and the Ewing family of tumors (EWS) in order to supplement histological diagnosis, which is difficult due to the tumors’ similar appearance. The accuracy of diagnosis is of paramount importance because the prognosis, treatment options, and responses to therapy vary widely across the four categories. The researchers used cDNA microarray data of 88 samples (63 for training and 25 for independent testing), containing 6,567 genes. After weeding out genes that produced very small expression values in the microarray experiment, 2,308 genes remained to be used for the analysis. The dimensionality of this data set was further reduced via PCA, with the first ten principal components (accounting for 63% of the variation in the expression data) to be used for scoring the expression data, thus resulting in a 10-dimensional input vector for each of the samples. The network architecture was chosen to be a simple two layer linear perceptron, with ten inputs and four threshold units. The network was trained using gradient descent with a learning rate of 0.7 and a momentum coefficient of 0.3, with calibration terminated after 100 iterations. Three-fold cross-validation was used, and the procedure was repeated 1,250 times, thus training a total of 3,750 ANNs, with the classifications in each of the validation samples being based on the committee vote of the 1,250 ANNs. The test samples, however, were classified using a committee vote from all of the 3,750 networks. Based on the 63 samples used for training, a 96 gene subset of genes deemed most relevant for classification was identified by a sensitivity analysis involving the evaluation of the partial derivative of each of the outcomes with respect to each of the 2,308 genes, taken as an absolute value and averaged over the four outcomes and over the 63 training samples. Following the extraction of the 96 relevant genes, ten principal components were again evaluated and the entire network training procedure was repeated. Using these 96 genes, the network achieved 100% correct classification on the independent test data.

Pal et al. was able to use a multilayer neural network, combined with “online” gene selection and fuzzy clustering, and the same SBCRTs dataset as Khan et al., to identify a set of seven genes that could be used for precise classification of the four tumor subgroups (49). In this application, the researchers use a feature selection MLP (FSMLP) which associates a gate with each of the inputs. This gate is in the form of an attenuating function which attenuates the input, prior to it going into the network, based on the ability of the input to reduce the training error. This attenuating function is differentiable with respect to the parameter which governs the attenuation, and thus can be optimized by a standard back-propagation gradient descent algorithm (as in Eq. [2]). The chosen MLP architecture contains one hidden layer with 150 nodes. The FSMLP was able to select 20 genes that were most relevant to the classification task. Twenty ANNs, with the gates removed, where trained with these 20 genes, with various weight initializations, and all 20 networks resulted in 100% accuracy on the training data. The FSMLP was then again used to further reduce the gene signature to ten most relevant genes, while a non-Euclidian relational fuzzy c-means (NERFCM) clustering algorithm (50) was applied to the 20 genes selected previously to identify positively correlated genes (i.e., to reduce redundancy in the gene signature). The clustering process resulted in the identification of 6 clusters among the 20 genes. Next, genes that were not in the list of the top ten (from the pool of 20) where discarded from the clusters, leaving only the genes with the largest “gate-opening” values. This process resulted in the identification of a 7-gene signature, which was able to achieve 100% test accuracy.

Chang et al., used ANN analysis to identify micro RNAs (miRNAs) predictive of tumor status, in particular, to discriminate between stage II colorectal tumors and normal tissue, with a goal of better patient stratification with respect to the recommendations for adjuvant therapy (51). In CRC, responses to therapeutic agents are often unpredictable, which reflects the heterogeneity of the disease and highlights the need for accurately phenotyping the tumors in order to enable better personalized therapies and thereby optimize therapeutic outcome. The authors comment that miRNAs target mRNA cleavage and translational repression, thereby governing cell differentiation, proliferation, and apoptosis, and argue that miRNA profiles may be more effective in disease classification than genomic profiles. In this study, the researchers use a three layer MLP, optimized via feed forward back propagation gradient descent, with “relative expression of miRNA” as the inputs and a binary classification (stage II tumor or control) as the output. Cross-validation was utilized to help select the proper amount of neurons in the hidden layer.

In order to identify the miRNA signatures most predictive of tumor status, the authors utilized ANN-based algorithms, coupled with an additive stepwise approach. The stepwise procedure starts by cycling through all the steps in network optimization and validation with one input, choosing the best input according to prediction error on the validation set, and then repeating the process with two inputs (one that was chosen as best in the previous step, and cycling through the remainder of miRNAs), and so on. Fifty “reshuffelings” were performed to assign the cases as follows: 60% training, 20% testing (i.e., used to monitor and stopped the training once the model was optimized), 20% validation (i.e., used to measure predictive error). Once the predictive miRNAs were identified, analysis proceeded by comparing the up/down regulation of these miRNAs across individual-matched tumor and normal tissue, using ANOVA and the t-test. The analysis resulted in the identification of a three miRNA signature (miR-139-5p, miR-31, and miR-17-92) predictive of tumor status in stage II CRC samples with a median accuracy of 100%.

Petalidis et al., used a dataset of 65 highly annotated tumors and a simple, single-layer perceptron, to accomplish grading of human astrocytic tumors, derive specific transcriptional signatures from histopathologic subtypes of astrocytic tumors, and assess whether these molecular signatures define survival prognostic classes (52). In this study, the problem of classification into three tumor grades was reduced to three separate classification problems. Genes selected for inputs were identified via the “signal to noise” method on the entire U133A slide genome. Training performance, as well as the optimal number of genes required for grading was determined via leave-one-out cross-validation. For each of the leave-one-out runs, genes were ranked in accordance with signal-to-noise (taken over all but the left out sample) and grading success rate was determined using increasing numbers of these ranked genes. These genes were aggregated into one set, in which 59 genes were left after the removal of redundancies. Hierarchical clustering revealed a clear pattern of distinction between the GB, AA, and A tumor grades, and defined three functional gene classes for the molecular tumor subtypes. One subtype included genes that were responsible for wound healing, extracellular matrix constituents, and cell adhesion, these were characteristic of the 4 GB grade. Another group was involved in cell signaling, protein biosynthesis, and cell cycle. Survival analysis was performed using the ANN assigned classes, which resulted in the categorization of survival groups consistent with those identified in hystopathological grading.

Fakoor et al., utilize a dimensionality reduction technique via an auto-associative form of learning, called deep learning (i.e., auto-encoder neural network) (53). An auto-encoder attempts to learn high level features by using inputs as outputs and utilizing a hidden layer with nonlinear transfer functions between the two (i.e., an autoencoder learns the identity function). In this study, the authors attempt to develop a more generalized version of a cancer classifier that can learn concise/high-level features from unlabeled data, and thus, has potential to be generalized to new cancer types without the redesign of new features. Unlike methods that require the input/training data to correspond to the particular cancer type in order for the appropriate label to be provided for learning, data for this classifier can be obtained by combining gene expression information from different tumor types, as long as the data is generated via the same platform for gene expression assessment. The approach proposed by the authors is comprised of two parts, the feature learning part and the classifier learning part. The feature learning phase is itself comprised of two parts. First, dimensionality is reduced via PCA, and principal component scores, as well as some randomly selected “raw” features are used in the sparse autoencoder that learns an approximation of the input data constructed by a limited number of the neurons in the hidden layer. This resulting network is trained via the back propagation gradient descent method with a sparsity penalty (54). The sparsity penalty forces the activations in the hidden layer to zero, thereby forcing the network to represent the inputs via a small number of the hidden layer activations. The authors argue that the result of sparse encoding of the input space, is that hidden layer “features that allow for a sparse representation are more likely to encode discriminatory functionally monolithic properties of the original data and thus are more likely to form a good basis for classification learning”. In the classifier training phase of the process, the activations from the hidden layer of the feature learning phase are used with a set of labeled data to train a three layer MLP softmax classifier (described above in the paper). The authors point to work by Lu et al., where the possibility of discovering common gene features across various cancer types was demonstrated (55). The classifier was evaluated using 10-fold cross validation and compared against results of two “baseline” algorithms [a supper vector machine (SVM) trained with Gaussian kernel, and regular softmax regression] for 13 different data sets. The classifier proposed by the authors outperformed the baseline algorithms for 11 out of the 13 datasets.

Revisit of the SRBCT dataset

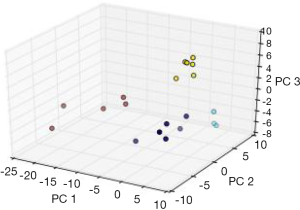
In order to conduct a simple experiment with the previously described feed forward MLP methodology, the authors constructed a neural network, with a soft-max classification output layer, and trained it to distinguish between the various types of SRBCTs, utilizing the data set from Khan et al. (48). As previously described in this paper, the data consists of 88 samples, 63 of which were used for training and 25 for testing the performance of the classifier. In the first step, using only the training set, all 2,308 significantly expressed genes were filtered (using ANOVA) for significant expression differences across tumor classes, and the top 100 (ranked in ascending order on basis of P values) were kept for PCA analysis. Training data was projected onto the first three components, which accounted for approximately 70% of the variance in the data. Only three components were selected in order to facilitate a graphical representation of neural network performance. A MLP, with one hidden layer (containing five neurons) and a four-class softmax output layer, was constructed and trained for 80 epochs utilizing the back propagation gradient descent algorithm (see Figure 2). The classifier was evaluated via the 20 test samples which were histologically diagnosed cancers of the types used for training the classifier. Tissue types that did not correspond to a type of SRBCTs (i.e., skeletal muscle tissue, prostate cancer, etc.) were not used in for testing classifier performance. The classifier was able to correctly classify all 20 of the histologically diagnosed SRBCTs. Figure 3 exhibits the separation of the test input instances, as classified by the MLP classifier.

Figure 2 Graphical representation of the feed forward MLP. The input layer contains four input nodes, three of which receive an input in the form of gene data projection onto a principal component, while the 4^th represents the bias term. The second layer (hidden layer) contains five nodes, each of which receives a weighted average of the inputs and the bias term and plugs them into a sigmoid activations function. The represent a vector of weights from layer j to be used in the i^th node (where the number of components in each vector corresponds to the number of inputs, not including the bias term), x⁽ⁱ⁾ represent a vector of inputs from the i^th layer, and b⁽ⁱ⁾ represent the bias term for layer i. The activation values from the hidden layer are fed via weighted connections into the output layer, where each of the four nodes corresponds to a tumor class. The nodes of the output layer are activated via the softmax function and the activation values at each output node correspond to the probability of a tumor belonging to a particular class, given the values of the input. MLP, multilayer perceptron.

Figure 3 ANN performance. Separation of inputs (from the input layer in Figure 2) into four tumor classes is distinguished by different colors (from the output layer in Figure 2). The figure provides a visual representation of the ability of the neural network to identify non-linear boundaries in three dimensional input space and correctly classify the inputs according to the relative location of the input with respect to the separating hyper-plane. ANN, artificial neural network.

Conclusions

ANNs are powerful tools in the domain of data analysis. Their reputations as accurate classifiers, robust predictors, and versatile approximation tools have remained strong. The power of neural network implementations has been enhanced by the ingenuity of a multitude of researchers who are constantly adapting currently developed methodologies to their domain of inquiry, as well as designing novel, more powerful implementations. As genomic data becomes cheaper and even more available than it is today, neural networks will continue to offer their robust and reliable structures for diagnostic, prognostic, and predictive software applications in the field of cancer genomics.

Acknowledgments

The authors appreciate the valuable insights into the field of cancer genomics that were provided by Dr. Dung-Tsa Chen (H. Lee Moffitt Cancer Research Center) throughout the composition of this manuscript.

Funding: None. No federal or industry support was received for the production of this review article. The authors include Andrew Oustimov and Vincent Vu.

Footnote

Provenance and Peer Review: This article was commissioned by the Guest Editors (Dung-Tsa Chen and Yian Ann Chen) for the series “Statistical and Bioinformatics Applications in Biomedical Omics Research” published in Translational Cancer Research. The article has undergone external peer review.

Conflicts of Interest: Both authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.3978/j.issn.2218-676X.2014.05.01). The series “Statistical and Bioinformatics Applications in Biomedical Omics Research” was commissioned by the editorial office without any funding or sponsorship. The authors have no other conflicts of interest to declare.

Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.

Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.

References

1. Fearon ER. Human cancer syndromes: clues to the origin and nature of cancer. Science 1997;278:1043-50. [PubMed]
2. Vogelstein B, Papadopoulos N, Velculescu VE, et al. Cancer genome landscapes. Science 2013;339:1546-58. [PubMed]
3. Fodor SP, Read JL, Pirrung MC, et al. Light-directed, spatially addressable parallel chemical synthesis. Science 1991;251:767-73. [PubMed]
4. Schena M, Shalon D, Davis RW, et al. Quantitative monitoring of gene expression patterns with a complementary DNA microarray. Science 1995;270:467-70. [PubMed]
5. Hynes NE, Lane HA. ERBB receptors and cancer: the complexity of targeted inhibitors. Nat Rev Cancer 2005;5:341-54. [PubMed]
6. Turner N, Grose R. Fibroblast growth factor signalling: from development to cancer. Nat Rev Cancer 2010;10:116-29. [PubMed]
7. Yun J, Rago C, Cheong I, et al. Glucose deprivation contributes to the development of KRAS pathway mutations in tumor cells. Science 2009;325:1555-9. [PubMed]
8. Ramaswamy S, Tamayo P, Rifkin R, et al. Multiclass cancer diagnosis using tumor gene expression signatures. Proc Natl Acad Sci U S A 2001;98:15149-54. [PubMed]
9. Nutt CL, Mani DR, Betensky RA, et al. Gene expression-based classification of malignant gliomas correlates better with survival than histological classification. Cancer Res 2003;63:1602-7. [PubMed]
10. Glas AM, Floore A, Delahaye LJ, et al. Converting a breast cancer microarray signature into a high-throughput diagnostic test. BMC Genomics 2006;7:278. [PubMed]
11. Chang HY, Sneddon JB, Alizadeh AA, et al. Gene expression signature of fibroblast serum response predicts human cancer progression: similarities between tumors and wounds. PLoS Biol 2004;2:E7 [PubMed]
12. Ludwig JA, Weinstein JN. Biomarkers in cancer staging, prognosis and treatment selection. Nat Rev Cancer 2005;5:845-56. [PubMed]
13. Descotes F, Dessen P, Bringuier PP, et al. Microarray gene expression profiling and analysis of bladder cancer supports the sub-classification of T1 tumours into T1a and T1b stages. BJU Int 2014;113:333-42. [PubMed]
14. Paik S, Tang G, Shak S, et al. Gene expression and benefit of chemotherapy in women with node-negative, estrogen receptor-positive breast cancer. J Clin Oncol 2006;24:3726-34. [PubMed]
15. Bild AH, Yao G, Chang JT, et al. Oncogenic pathway signatures in human cancers as a guide to targeted therapies. Nature 2006;439:353-7. [PubMed]
16. Johannessen CM, Boehm JS, Kim SY, et al. COT drives resistance to RAF inhibition through MAP kinase pathway reactivation. Nature 2010;468:968-72. [PubMed]
17. Dellaire G, Berman JN, Arceci RJ. eds. Cancer Genomics: From Bench to Personalized Medicine. Academic Press: San Diego, 2014.
18. National Cancer Institute: PDQ Genetics of Breast and Ovarian Cancer. Bethesda: National Cancer Institute. Available online: http://cancer.gov/cancertopics/pdq/genetics/breast-and-ovarian/HealthProfessional
19. Zhao S, Fung-Leung WP, Bittner A, et al. Comparison of RNA-Seq and microarray in transcriptome profiling of activated T cells. PLoS One 2014;9:e78644 [PubMed]
20. Harrington CA, Rosenow C, Retief J. Monitoring gene expression using DNA microarrays. Curr Opin Microbiol 2000;3:285-91. [PubMed]
21. Patterson TA, Lobenhofer EK, Fulmer-Smentek SB, et al. Performance comparison of one-color and two-color platforms within the MicroArray Quality Control (MAQC) project. Nat Biotechnol 2006;24:1140-50. [PubMed]
22. Mardis ER, Wilson RK. Cancer genome sequencing: a review. Hum Mol Genet 2009;18:R163-8. [PubMed]
23. Golub TR, Slonim DK, Tamayo P, et al. Molecular classification of cancer: class discovery and class prediction by gene expression monitoring. Science 1999;286:531-7. [PubMed]
24. Tinker AV, Boussioutas A, Bowtell DD. The challenges of gene expression microarrays for the study of human cancer. Cancer Cell 2006;9:333-9. [PubMed]
25. Simon R, Radmacher MD, Dobbin K, et al. Pitfalls in the use of DNA microarray data for diagnostic and prognostic classification. J Natl Cancer Inst 2003;95:14-8. [PubMed]
26. Chen HY, Yu SL, Chen CH, et al. A five-gene signature and clinical outcome in non-small-cell lung cancer. N Engl J Med 2007;356:11-20. [PubMed]
27. Breslow LA, Aha DW. Simplifying decision trees: A survey. Knowl Eng Rev 1997;12:1-40.
28. Finak G, Bertos N, Pepin F, et al. Stromal gene expression predicts clinical outcome in breast cancer. Nat Med 2008;14:518-27. [PubMed]
29. Rish I. An empirical study of the naive Bayes classifier. In IJCAI-01 workshop on “Empirical Methods in AI” Key 2001;3:41-6.
30. Guyon I, Weston J, Barnhill S, et al. Gene selection for cancer classification using support vector machines. Mach Learn 2002;46:389-422.
31. Iorio MV, Ferracin M, Liu CG, et al. MicroRNA gene expression deregulation in human breast cancer. Cancer Res 2005;65:7065-70. [PubMed]
32. Cowan JD. Neural networks: the early days. In: Touretzky D. eds. Advances in Neural Information Processing Systems 2. Morgan Kaufmann: San Mateo 1990;828-42.
33. Fine TL. eds. Feedforward Neural Network Methodology. Springer-Verlag: New York, 1999.
34. Jain AK, Mao J, Mohiuddin KM. Artificial neural networks: A tutorial. IEEE Computer 1996;29:31-44.
35. Hinton GE. How neural networks learn from experience. Sci Am 1992;267:144-51. [PubMed]
36. Rummelhart DE, Hinton GE, Williams RJ. Learning representations by back-propagating errors. Nature 1986;323:533-6.
37. Ng AY. Unsupervised feature learning and deep learning. Available online: http://ufldl.stanford.edu
38. Bishop CM. Neural networks and their applications. Rev Sci Instrum 1994;65:1803-32.
39. Rumelhart DE, McClelland JL, PDP Research Group (1986). Parallel Distributed Processing: Explorations in the Microstructure of Cognition, Volumes 1 and 2. MIT Press: Cambridge, 1986.
40. Bishop CM. eds. Neural Networks for Pattern Recognition, Clarendon Press: Oxford,1995.
41. De Freitas JF. Bayesian methods for neural networks. Doctoral dissertation: University of Cambridge, 2003.
42. Kung SY, Luo Y, Mak MW. Feature selection for genomic signal processing: Unsupervised, supervised, and self-supervised scenarios. J Signal Process Sys 2010;61:3-20.
43. Sanchez-Carbayo M, Socci ND, Lozano JJ, et al. Gene discovery in bladder cancer progression using cDNA microarrays. Am J Pathol 2003;163:505-16. [PubMed]
44. Takamizawa J, Konishi H, Yanagisawa K, et al. Reduced expression of the let-7 microRNAs in human lung cancers in association with shortened postoperative survival. Cancer Res 2004;64:3753-6. [PubMed]
45. Tusher VG, Tibshirani R, Chu G. Significance analysis of microarrays applied to the ionizing radiation response. Proc Natl Acad Sci U S A 2001;98:5116-21. [PubMed]
46. Ding C, Peng H. Minimum redundancy feature selection from microarray gene expression data. J Bioinform Comput Biol 2005;3:185-205. [PubMed]
47. Saeys Y, Inza I, Larrañaga P. A review of feature selection techniques in bioinformatics. Bioinformatics 2007;23:2507-17. [PubMed]
48. Khan J, Wei JS, Ringnér M, et al. Classification and diagnostic prediction of cancers using gene expression profiling and artificial neural networks. Nat Med 2001;7:673-9. [PubMed]
49. Pal NR, Aguan K, Sharma A, et al. Discovering biomarkers from gene expression data for predicting cancer subgroups using neural networks and relational fuzzy clustering. BMC Bioinformatics 2007;8:5. [PubMed]
50. Hathaway RJ, Bezdek JC. NERF c-Means: Non-Euclidean relational fuzzy clustering. Pattern Recognition 1994;27:429-37.
51. Chang KH, Miller N, Kheirelseid EA, et al. MicroRNA signature analysis in colorectal cancer: identification of expression profiles in stage II tumors associated with aggressive disease. Int J Colorectal Dis 2011;26:1415-22. [PubMed]
52. Petalidis LP, Oulas A, Backlund M, et al. Improved grading and survival prediction of human astrocytic brain tumors by artificial neural network analysis of gene expression microarray data. Mol Cancer Ther 2008;7:1013-24. [PubMed]
53. Fakoor R, Ladhak F, Nazi A, et al. Using deep learning to enhance cancer diagnosis and classification. Proceedings of the 30th International Conference on Machine Learning, JMLR: W&CP;2013;28.
54. Raina R, Battle A, Lee H, et al. Self-taught learning: transfer learning from unlabeled data. In: Proceedings of the 24th International Conference on Machine Learning. ACM, 2007;759-66.
55. Lu Y, Yi Y, Liu P, et al. Common human cancer genes discovered by integrated gene-expression analysis. PLoS One 2007;2:e1149 [PubMed]