
Integrative clustering methods for high-dimensional molecular data
Introduction
Identification of molecular subtypes of cancer using high-throughput genomic data has received a great deal of attention in the current literature (1,2). Traditionally, cancer subtype diagnosis has been based on non-molecular, clinicopathologic parameters such as the morphological and functional characteristics of the cancer cells. However, classification criteria defined using such technologies may not be sufficient and likely overly general as patients with the same cancer diagnosis can differ significantly in their response to treatment and long term prognosis (3). These differences have been hypothesized to arise as a result of molecular heterogeneity at genomic, epigenomic, transcriptomic, and proteomic levels, and efforts to exploit such molecular data for the discovery of novel, clinically relevant cancer subtypes, have grown rapidly in the past decade. For example, molecular heterogeneity within individual cancer subtypes has been demonstrated in the variable presence of chromosomal translocations, deletions/insertions of tumor suppressor/inhibitor genes and numerous chromosomal abnormalities (4). More recently, microarray based gene expression data has been used to identify tumor subtypes across numerous cancer types (5-7), and the molecular subtypes identified through such efforts have been shown to correlate with clinically important endpoints, such as disease prognosis and response to treatment. Specifically, Sørlie et al. (1) used gene expression patterns of breast cancer carcinomas to distinguish tumor subclasses. Lapointe et al. (5), used gene expression profiling in order to identify subtypes of prostate cancer. Also given the plasticity of epigenetic modifications and their role in controlling gene expression and expression potential, there has been significant interest in the use of epigenomic data to identify novel tumor subtypes (8-10).
Cancer subtype discovery using different omic data types is the most frequently facilitated through use of clustering. While there exists countless different clustering methodologies, the objective is the same and involves the grouping of objects across a discrete set of classes (i.e., clusters), such that objects within the same class are more similar to one another compared to objects in different classes. In the context of transcriptomic data, clustering methods can be used to cluster either genes or samples: (I) if applied to genes, clustering results in classes with similar gene expression levels across the samples, enabling the identification of biological pathways or gene expression networks; (II) if applied to the samples, clustering results in classes of subjects that share a similar expression across the panel of genes. In this review we focus our attention on the clustering of samples with goal of identifying molecular subtypes of disease.
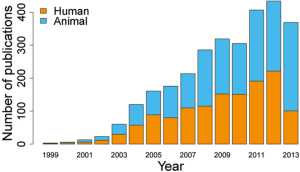
Cancer is a complex disease that manifests as a result of coordinated alterations on the genomic, epigenomic, transcriptomic and proteomic levels. This, along with the decreasing cost of high-throughput techniques has served to motivate integrative genomic studies; studies involving the simultaneous investigation of multiple different omic data types collected on the same set of patient samples. One of the research networks established to generate the comprehensive catalogue of genomic abnormalities is The Cancer Genome Atlas (TCGA). TCGA is sponsored by NCI and NHGRI and represents a coordinated effort aimed at exploring genomic alterations and interactions across biological assays in the context of human cancer. TCGA collects and analyzes tumor samples and makes the data freely available for researchers to use. Integrative genomic research has received a great deal of attention in recent years and the number of research publications in this area has been steadily increasing as shown by recent PubMed data (result of PubMed data search with key word “Integrative Genomics”) (Figure 1). The growing interests in integrative analyses indicate that the multi dimensional characterization of the genomic features will soon be standard practice. Comprehensive and coordinated analytic methods that can utilize all such information in a single comprehensive analysis are very important in order to understand the molecular basis of cancer and their subtypes. The goal of this paper is to review several non-integrative clustering methods and three recently proposed integrative clustering methods using; (I) joint latent variable model (11); (II) non negative matrix factorization (NMF) (12) and Gaussian mixture model (13).
Clustering methods
A clustering is a collection of objects that are more similar to each other within a group compared to objects between the groups. Microarrays generate datasets, such as gene expression or methylation signals, which results in a set of m features assayed across n samples; generally m is larger than n. More formally, clustering of samples can be defined as a method of determining a classification of the n subjects into K discrete classes (K << n) for a given dataset X = {x1,x2,x3,…,xn}, with each subject xi, i=1,2,…,n characterized by m features, xi = (xi1,xi2,…,xim). The main aim of clustering is to discover and describe the underlying structure in the data.
Clustering methods for a single data type at a time
Several clustering methods have been developed that consider single data type at a time (14-16) and a few methods that consider multiple types of the datasets simultaneously (11-13). However, the choice of the appropriate clustering methods for a given data (or datasets) is far from straightforward. The choice is often subjective and generally driven by the context of the study and characteristics of the data under examination (17). In the context of genomic studies, clustering methods consider the molecular profile, such as gene expression or DNA methylation, either considering the datasets separately or together, to identify the subtypes based on some dissimilarity criteria. Following clustering, the resultant clusters are then typically compared with regard to clinical characteristics collected on the study subjects (e.g., survival time, time to recurrence, progression) as a means for understanding their phenotypic importance. A plethora of algorithms has been developed in the literature that considers one data at a time. We describe a few of them as follows:
K-means clustering
K-means clustering method partitions the samples into k clusters given the data points and k number of centroids in an automated fashion (18). This is one of the most widely used classification algorithm both in microarray and other studies such as engineering and computer science. Typically, the method partitions the subjects making sure that the inter cluster distances are maximized and within cluster distances are minimized. The intended number of clusters (k) is determined to initialize the algorithm and k centroids as cluster centers are randomly selected. The samples are assigned to clusters within the nearest centroid using the defined distance and new centroids are calculated as an average distances between the old centroid and subjects in that cluster. This process is repeated until the samples stop changing the cluster assignment (19). K-means clustering methods have been used in the studies of tumor types (19). Extended version of k-means method that accounts for the geometrical complexity of the data has been used in Kim et al. (20).
The main disadvantage of the K-means clustering method is that it requires initial guess of the number of clusters and also is highly dependent on the centroids initialized at the beginning leading to a local minimum solution. Another problem with K-means clustering is that it does not account for variance in the data. Also, the frequently used Euclidean distance places the highest influence on the largest distance which causes lack of robustness against outliers that result in large distances. To resolve this issue, instead of assigning the most centrally located sample, medoids can be specified which is called k-medoids or partition around the medoids (PAM) (21). Again, k-medoids method requires initial guess of the number of clusters which we generally do not know. Inappropriate choice of k can result in poor results.
Hierarchical clustering
Hierarchical clustering is probably the most widely used clustering method in biological studies. This method constructs a hierarchy of nested clusters which does not require cluster number specification as in K-means method. As the name suggests, the method produces hierarchical representations in which the clusters at each level of hierarchy are created by merging clusters at next lower level. At the highest level there is only one cluster and, at the lowest level, each cluster contains a single observation (18). Therefore, this method requires a study-specific (user defined) threshold in order to get meaningful clusters. The graphical display of the entire process is called the dendogram and is often viewed as a graphical summary of the data. Hierarchical clustering has successfully been able to identify clinically relevant tumor subtypes in the previous several studies (4,6,22,23).
There are two types of hierarchical clustering methods: agglomerative and divisible. The agglomerative, also known as bottom up, merges the sample points iteratively to make clusters within the similarity distance. The divisible which is also known as top down starts with all the samples and subdivides them into smaller groups iteratively. The hierarchical clustering methods vary with respect to choice of the distance metric and cluster merging known as linkage. The calculation of the distances between two clusters is based on the dissimilarity between the samples from the two clusters. The commonly used distances between the two clusters is the average linkage method. In this method the distance between the two clusters 1 and 2 is defined as the average of all distances between each element in cluster 1 and each element in cluster 2. Other distance methods used are single linkage (or nearest neighbor) and complete linkage (or furthest neighbor). In single linkage method, the distance between cluster 1 and cluster 2 is the shortest distance from any member of cluster 1 to any member of cluster 2. In contrast, the complete linkage method defines the maximum distance from any member of cluster 1 to any member of cluster 2. Thus, in the presence of outliers, using single linkage, those outliers are accounted at last while using complete linkage the outliers are considered at first. Therefore, average linkage is commonly used to avoid this sensitivity to outliers and the resulting clusters are based on the average density. Besides these, the distance between the centroids or medoids of clusters is also used.
The advantage of this approach is that the end results can easily be visualized, from which, coordinately regulated patterns can be relatively easily discerned by eye (24). One of the drawbacks of such methods is that, as they are carried out in several stages, the possible mis-clustering at the one stage cannot be corrected in the subsequent stages and even magnifies as the process progresses, i.e., there is no compensation for the greedy nature of the algorithm (25). Therefore when n is large, accumulation of the mis-clustering will be huge resulting in lack of robustness. Also, the developed tree structure is highly sensitive to the distance metric used to assess similarity and requires subjective evaluation to define the clusters which can differ from person to person.
Fuzzy C-means clustering
Unlike general clustering techniques which exclusively assigns each sample to a single cluster, this method allows samples to be members of more than one clusters thus resulting in overlapping clusters (26,27). The fuzzy C-means clustering algorithm is a variation of the k-means clustering algorithm, in which a degree of membership of clusters is assigned for each data point (28). The membership is assigned with a weight ranging from 0 to 1 where 0 implies excluding from the cluster and 1 implies including in the cluster. Other weights, 0< wi <1, implies probability of including the sample in that cluster. The membership weight for a cluster member is determined as the proportion of its contribution to the cluster mean. Such membership values are iteratively recalculated (adjusted) until the change between the two iterations falls below a pre-specified threshold. As the method permits the samples to be in more than one cluster, it is called fuzzy clustering.
Similar to the many other methods, fuzzy C-means method can be used to cluster the subjects as well as genomic features. This method has especially been recommended for clustering the genomic features that are considered noisy and are equally likely to belong to more than one cluster (27). However, this method suffers from the similar drawbacks of K-means method as the fuzzy algorithm is similar in computation to that of K-means algorithm. In addition, this method requires estimation of the fuzziness parameter but there is no general consensus on the estimation or specification of such parameter.
Self organizing map (SOM)
SOM was originally developed to apply in neural network studies (29,30) but, in recent years, this has been used in pattern identifications of gene expression datasets as well (31-34). SOM allows partial structure on the clusters as opposed to no structure of K-means clustering and rigid structure of hierarchical clustering enabling intuitive visualization and clustering. The algorithm starts with selecting geometry of nodes (cluster centers) usually in two dimensional grids, called map. The nodes are then randomly mapped to k-dimensional space of the data and then iteratively adjusted. At each iteration, a data point P is selected randomly from the data and the nodes are adjusted by moving towards that data point. The movements of the nodes are proportional to its distance from the data point; the closest node moves most followed by other nodes. The magnitude of movement decreases per iteration. The process is repeated until the movements stabilize or a fixed number of iteration is used. In this way, the neighboring points in the initial geometry are mapped in k-dimensional space.
The advantage of SOM is that it reduces the computational complexity as the optimization is restricted to lower dimensional space (typically two dimensional). Also, SOM provides natural way of obtaining the clusters based on the initial input geometry. However, it is difficult to come up with appropriate input nodes and may result in non-convergence problem of the algorithm. Also, SOM is sensitive to choice of number of nodes like K-means method.
Tight clustering
Tight clustering is a resampling based approach for identification of tight pattern in the data and is especially appropriate for the data having potential outliers (35). The method utilizes the subsampling technique to create variability enabling to distinguish the scattered samples from the samples inherently tightly clustered together. The scattered points are not necessarily forced to be in the clusters in the subsequent steps. K-means clustering is used as an intermediate step in the tight clustering where the initial values for the k-means algorithm can be derived from Hierarchical clustering. After series of subsampling and clustering is carried out, a tight and stable cluster is identified which is then removed from the data and the iteration is continued to identify second cluster and so on.
The method is an appealing with application in microarray data as the method allows highly scattered points without being clustered (36). However, the method has the potentiality of suffering from the same drawback of k-means algorithm. Also, since all the data points are not necessarily included in clustering, the method can not address the possibility of importance of the abandoned points.
Model based clustering
Model based clustering assumes that the data follows mixture of known distribution such as Gaussian distribution (37-40). The problem of selecting the good number of clusters and the class memberships of the individuals are carried out as model selection problems in the probability framework (41). In essence, the method defines clusters as sub-groups following the specified distribution. Likelihood function of the mixture model is defined and expectation maximization (EM) algorithm is used to find the clustering assignments maximizing the likelihood. In addition, a few algorithms use the Bayesian Information Criteria (BIC) (42) as an optimization criterion to suggest optimum number of clusters.
An advantage of this approach is that it has statistically more solid foundation for estimation and model selection which is more suitable framework for statistical inference and interpretation. However, the distributional assumptions are difficult to justify for high dimensional datasets in general. Although some transformations have been suggested to transform the data into known distribution, it is difficult to identify correct transformation function. As a result, the method may result in spurious clusters due to the lack of satisfying distributional assumptions and possible local minima in the optimization of the likelihood.
Non negative matrix factorization (NMF)
NMF is a dimension reduction technique that factorizes a non negative matrix into two non-negative matrices (43-45). The idea behind the NMF is that, for a given data, either a factor is present with a certain positive effect or it is absent simply having a zero effect. Suppose is a non-negative data with n samples and p features. Then, NMF approximately factorizes the matrix into two non-negative matrices and
where is the matrix of basis vectors with n samples and k groups (pre-assigned) and is the matrix of coefficient vectors with k groups and p features. Each column of X can be written as where x and h are the corresponding columns in X and H respectively. Each data vector x is approximated by a linear combination of the columns of W weighted by the components of h. Therefore W is regarded as a matrix of basis vectors which is optimized for the linear approximation of the data in X (44). In order to approximate the optimum factors several objective functions (also called cost functions) have been proposed but the most frequently used is based on Euclidean distance as defined by,
W and H are initialized and the objective function is minimized iteratively until convergence. A drawback of this algorithm is that the function F is convex in W only or H only but not on both when considered together. Therefore, there is a possibility of ending up with local minima instead of global minima. To avoid this problem several different initializations with multiple repetitions of the algorithm has been proposed. The most important characteristic of NMF is that it reduces the data set from its full dimensionality to a lower dimensional space and identifies patterns that exist in the data using only the subset of the data.
Lee and Seung (44) proposed one of such algorithms and pointed out the application of NMF on the pattern recognition and its efficacy comparing with traditionally used singular value decomposition (SVD) or principal component analysis (PCA). They used the algorithm to decompose human faces into part-features such as eyes, nose, ear etc. In that study context, they noted that NMF was able to differentiate the features and were visually clear. In contrast, they noted that the use of PCA to the image data yielded components with no obvious visual interpretation. The reason behind such contrasting results was described in terms of the disparities of the constraints imposed on the linear combination. As NMF imposes the non negativity constraint, the linear combination has only the additive effect, if the effect is present, and is likely to be compatible with the intuitive notion of combining parts to form whole. But, the mixture of positive and negative signs in the linear combination of SVD or PCA may create subtractive effects for some important features and therefore may not always be discernible.
NMF method has been successfully used in the microarray datasets (12,15,45,46). Brunet et al. (15) utilized the NMF technique in the gene expression data from a leukemia study to find the cancer subtypes. The algorithm as proposed by Lee and Seung (44) was used on the gene expression data Xn×p in order to obtain Wn×k and Hk×p where n, p and k represent number of samples, number of genes and number of clusters respectively. To determine the cluster membership, the maximum value of each row of matrix W is used. For example, suppose the first row of W has the maximum value in the 2nd column. Then the first sample is assigned for the 2nd cluster.
The most important part of the method proposed by Brunet et al. is the estimation of the optimum number of clusters, k. They utilized consensus clustering (47) and cophenetic correlation to determine k as follows: For each run of the algorithm, a connectivity matrix C of size n×n is defined based on the sample assignment to the clusters. If two samples i and j belong to the same cluster then the corresponding entry of the connectivity matrix is 1 (cij =1) otherwise it is 0 (cij =0). Consensus matrix, , is computed as an average of the connectivity matrices over the many clustering runs until convergence. The entries of, ranging from 0 to 1, reflects the probability of clustering the samples i and j together. Then, , the distance between the samples induced by the consensus matrix is computed. In parallel, using average linkage HC on , the distance between the samples induced by the linkage used in the ordering of is computed. Then, Pearson correlation is computed between the two results which is called the cophenetic correlation (ρk). The process is repeated for each pre-assigned k and the value of k that results in maximum ρk is chosen as optimum k. However, the method proposed by Brunet considers one data type at a time. For other details of the algorithm see Brunet et al. 2004 (15).
Clustering multiple datasets
The recent development of high throughput genomic technologies have generated several types of genomic datasets on same set of patient samples, e.g., mRNA expression, DNA methylation, DNA copy number etc. The interaction of biological processes manifesting in different data types measured by such genomic assays can have important implications for disease development and progression. Therefore it is important to take into account the multiple datasets together in order to optimize strength of biological information across multiple assays relevant to the disease of interest. Traditionally, approaches for clustering samples based on multiple ‘omic’ datasets have involved the manual integration of results obtained from the individual clustering of each of ‘omic’ data types. Such methods require great deal of understanding of all the data types and the biology associated with them in order to fully utilize the available information. Although such approaches will be able to capture the strong effects across multiple data types, there may be weak but consistent genomic alterations present across the data types which will be equally informative. Such genomic variation may be missed by separate analyses followed by manual integration. In addition, this approach is tedious, ad hoc and can be inconclusive in the assignment of subjects to molecular cancer subtypes.
These problems can be addressed by the use of fully integrative clustering techniques. One such approach is iCluster (11), which uses a joint latent variable model within a likelihood framework with an L1 penalty to produce a “sparse” solution. A second example of integrative subtype detection is by Zhang et al. (12) that identifies common correlated subsets across the multiple data sets termed as multi-dimensional module. However the focus of this method is to identify the multi-dimensonal module rather than finding the unique clusters of samples based on the genomic data. Another example of integrative clustering is the mixture model based method proposed by Kormaksson et al. (13). These methods are briefly discussed below.
Integrative clustering of multiple data types using iCluster
Shen et al. (11) proposed a joint latent variable model for integrative clustering of multiple genomic datasets. This method models the tumor subtypes as an unobserved latent variables which are simultaneously estimated from the multiple data types. The key idea of the method is based on two previous works by Tipping et al. (48) and Zha et al. (49). Tipping et al. showed that the principal axes of a set of observed data, in PCA, can be determined through maximum likelihood estimation of parameters in the Gaussian latent variable model which is closely related to factor analysis. In Gaussian latent variable model the correlations among the variables are modeled through the latent variables with additional term for the residual variance.
where X is the mean centered matrix of p features with n samples, Z is matrix of latent variables, W is the coefficient matrix and k is number of clusters. Thus and the model parameters are determined using maximum likelihood method using EM algorithm (50). Important point to note here is that the maximum likelihood estimates of the columns of W in general do not correspond to the principal subspace of the data. Tipping et al. showed that assuming the isotropic error model with covariance matrix , the maximum likelihood estimation of W has connection with the PCA. They further established that the posterior mean of the latent factor Z conditional on the data is a function of W and σ2 and represents the principal axes of the data.
Zha et al. (49) proposed alternative algorithm of the K-means clustering by using PCA of the gram matrix of the data. They reformulated minimization of the within cluster squared distance as used by k-means algorithm to a maximization of trace of . They showed that the trace maximization problem has a closed form solution and corresponds to Z equal to largest eigenvectors of . Such eigenvectors give rise to first principal axes of the data. Zha et al. (49) further mentioned that such matrix of eigen vectors Z of dimension can be considered as a transformation of the original data of n dimensional space into new dimensional subspace and can be considered as a cluster indicator matrix. Then, they suggested QR decomposition or the k-means algorithm on the cluster indicator matrix to compute the cluster assignment for the samples.
Shen et al.’s (11) method uses the principals of these two methods and extends the algorithm of Tipping and Bishop to integrative clustering of the multiple data types. The method computes the posterior mean of the latent factor matrix Z given data using Gaussian latent variable model and uses the standard k-means algorithm to compute the cluster membership. In addition they incorporate the shrinkage and feature selection technique using least absolute shrinkage and selection operator (Lasso) type penalty function. Lasso (51) is a shrinkage method which sets some of the small coefficients (likely non-informative features) to exact zero while other bigger coefficients shifting towards zero using a threshold, λ, called tuning parameter. The idea behind using the shrinkage is to classify the samples based on important features only, reducing the possible noise. The basic steps of the implementation of the algorithm can be summarized as follows:
Suppose are m data types on the same set of subjects with dimensions, where are number of features in each dataset and n is the number of samples. Then the mathematical form of the integrative model can be given as
where Wi is the coefficient matrix of dimension and Z with dimension is the latent variable component that connects m sets of models inducing dependencies. The latent variable is intended to explain the correlations across the data types and ɛi’s represent the remaining variances that are unique to each data types. The integrated data matrix is then multivariate normal with mean zero and covariance matrix . Then the log-likelihood function is defined imposing L1 penalty on W and EM algorithm is used to estimate the parameters. The latent variables Z are considered as missing and estimated in the expectation step of the algorithm that are then updated in the penalized maximization step. The posterior mean of the latent factor, , is estimated and then standard K-means clustering algorithm is used on to draw inference on cluster memberships. The tuning parameter, λ, for the L1 penalty function and optimum number of clusters, k, are estimated by minimizing the proportion of deviance (POD) where the POD is defined as the sum of absolute differences between the product of posterior mean of latent factors given data (Standardized) and perfect diagonal block structure. Shen et al. (52) also propose alternative method of choosing the tuning parameter using sub-sampling technique. In this method the data is repeatedly partitioned into training and testing datasets. The algorithm is used in the training set to estimate the parameters and then utilized to predict the cluster membership in the test set. The algorithm is also utilized in the testing set in parallel and the cluster membership is obtained. Then the agreement index is computed between the two clustering assignments and maximized to obtain set of tuning parameter λ, and number of clusters, k. In recent work of Shen et al. (52), flexibility of using two more penalty functions, elastic net (53) and fused lasso (54), has been provided in addition to lasso.
The method proposes appealing approach of integrative clustering analysis incorporating the variable selection feature in the algorithm. Capturing the correlation across the multiple data types in the form of latent variable, this method nicely integrates several datasets collected on the same patient samples simultaneously. The drawback of the method is that if the assumption of the isotropic error model is not satisfied, optimum solution may not be obtained. Also, as k-means algorithm is used for the cluster membership at the end, the method still possibly share the drawbacks of k-means algorithm.
Integrative clustering of multiple data types using non-negative matrix factorization
Zhang et al. (12) extended the algorithm proposed by Lee and Seung (44) for the multiple data types in a single comprehensive clustering analysis. The purpose of their algorithm is to identify the subsets of multidimensional genomic data that have correlative profiles, termed as multidimensional module (md-module), across several types of measurements on the same samples. The first step of the algorithm involves the joint factorization of the data sets. Suppose, are datasets with dimensions respectively where n represents the number of samples and pi represents the number of features. Then the joint factorization is carried out as
where is the basis matrix which is common across the multiple data types and are the coefficient matrices specific to each data type separately. The matrices W and Hi’s are estimated by minimizing the objective function given by min for , where W and Hi’s are initialized multiple times and updated separately until convergence in order to get the optimum solution. For details of the algorithm, see Zhang et al. (12).
After W and Hi’s are estimated, in the next step, correlated subsets are estimated based on both samples and features. To determine the md-module, z-scores are computed for each element of the matrices Hi’s by row. Then a data driven (or user defined) threshold T is identified and the z-scores greater than the threshold are assigned to be in the md-module. Similarly, for the clinical characterization, the samples are divided into two groups, module specific and non module specific, by using W. Z-scores for the elements of W are computed by column and again data driven (or user defined) threshold is utilized for grouping. Clinical differences between the identified groups are assessed using several statistical methods, such as survival analysis using Kaplan-Meier curves and log-rank tests.
This method is focused on finding the correlated substructure across the multiple data types in which some features can belong to multiple modules while others may not belong to any. Therefore, this does not cluster the samples (or features) exclusively assigning each sample into unique clusters. However, this method identifies the correlated subsets reducing the dimensionality of the multiple data sets simultaneously.
Mixture-model based integrative clustering of multiple data types
Kormaksson et al. (13) proposed a model based clustering method imposing specific Gaussian mixture distribution on each cluster. The method constructs likelihood for any given partition of the subjects and the estimation is carried out using EM algorithm. The method has been formulated initially for a single data type specifically considering methylation data, although in general any other microarray data sets can be used. Then the method has been extended to multiple data types in a single comprehensive analysis. One of the strong assumptions of this method is that each probe set j can be dichotomized as high and low signal groups for each patient i and then two-component Gaussian mixture model can be applied for each patient. Suppose, C is the true partition of the n samples and for each cluster , there is latent indicator vector such that if probe set j has high signal for all subjects in cluster c otherwise . Another assumption is that all subjects in cluster C have similar relative signal status (high/low) for probe set j. Then the density of data , conditional on the unobserved latent variable w with parameter , is given by
The density for each subject is modeled as two component Gaussian mixture model as , where φ denotes normal density. Bernoulli prior is specified on the latent variable w with density,
where and represent the proportions of probe sets having high and low signal status respectively. Then joint density is integrated with respect to latent variable
This likelihood function is used as an objective function and the parameters are estimated using EM algorithm. In order to avoid the problem of local maximization, multiple initializations of the parameters is suggested and the parameter values corresponding to the maximum of the likelihood are chosen.
The likelihood is extended to multiple datasets as long as the datasets satisfy the similar model assumptions as defined for the single data type, i.e., the subjects in a given cluster have correlated signal profiles across multiple data types (e.g., high methylation and low expression or low methylation and high expression etc.). The likelihood function is derived as before with an additional product term across m data types. Kormaksson et al. (13) have proposed two algorithms to find out the optimum partitions; (I) hierarchical clustering; and (II) iterative clustering. Hierarchical clustering algorithm is intended to come up with good candidate partition and iterative clustering algorithm is to improve upon the initial partition.
The hierarchical algorithm starts with the partition where each subject represents its own cluster. The likelihood is defined considering two-component Gaussian mixture model for each of the n subjects. EM algorithm with several initializations is used to estimate the optimum parameters. Next, the likelihood is defined merging two subjects in ways and is optimized using EM algorithm as before. Then three subjects are merged and the process is continued until single cluster is left. The partition that has highest value of the corresponding likelihood is chosen as final clusters.
In order to run the iterative clustering algorithm, cluster membership indicators are defined for each subject i as if subject i is in cluster C and otherwise. Then assuming and are independent and identically distributed with multinomial distribution, the density of X is defined as where . The classification likelihood given the membership indicators Xi’s is defined as . Multiplying and integrating out X, the marginal likelihood is given as where . Initial partition X(0) is computed using hierarchical algorithm and then updated iteratively in order to maximize the likelihood using EM algorithm. Once the optimum parameters are estimated, the subjects are assigned the clustering membership by computing the posterior expectation . Each subject is assigned to the cluster to which it has the highest estimated posterior probability of belonging.
The method provides an attractive framework for integrative model based clustering. One of the novelties of the method is that it models the subject specific parameters. This enables the method to work in typical genomic data in which number of features exceeds the number of subjects. Since the method does not perform automatic feature selection, the user has to pre-select the features based on some criteria such as most variable features or features that are significantly associated with phenotype of interest. Also, the model assumptions that are uniquely defined for this method have to be met in order for this method to work. The method has been extensively described in the context of microarray methylation and expression data sets but the applicability of the method in non-microarray platforms has yet to be assessed.
Although the purpose of all three methods is to utilize correlated information across the several genomic assays on the same set of samples in order to better understand the disease, the implementation of the methods are based on separate statistical framework. Application of iCluster and Gaussian mixture model based methods (sections 4.1 and 4.3) require their model assumptions to draw valid conclusions while NMF based method (section 4.2) does not rely on any model assumptions. iCluster and model based methods classify the samples in such a way that each sample can fall in unique cluster while in NMF based method a samples can fall in more than one subset or can be completely excluded based on the correlation structure in the data. In addition, iCluster has automatic feature selection step through the use of lasso penalty while other two methods do not have that.
Data and examples
Publicly available data on ovarian cancer from TCGA project was used to describe the clustering methods mentioned in this paper. The data sets we used consist of Agilent gene expression data (90,797 probes) and DNA methylation data (27,338 probes) with clinical outcomes on 499 subjects. In order to reduce the dimensionality of the data sets, top thousand probes from each of the gene expression and methylation data were selected by running Cox proportional hazards model for each gene and methylation probes with time to recurrence of disease as end point adjusting for age and cancer stage. The datasets with these selected probe sets were used further in the clustering methods. The examples presented in this paper are intended to illustrate the clustering methods discussed in the paper rather than serving as substantive analyses.
Single data clustering methods
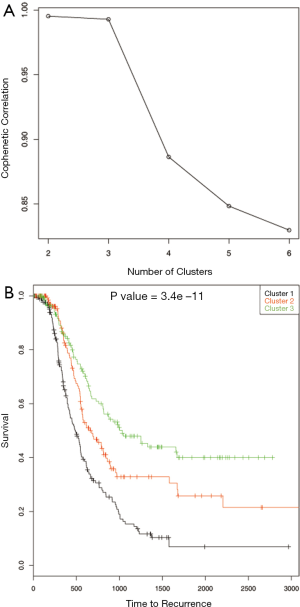
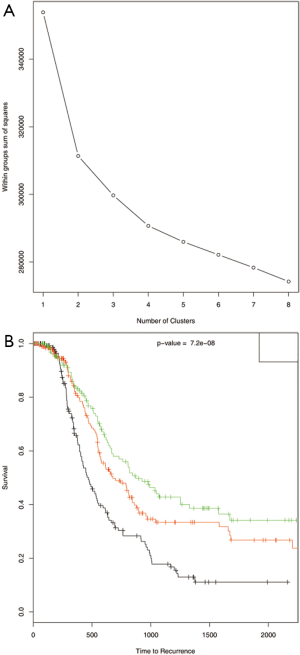
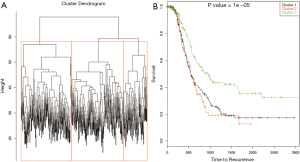
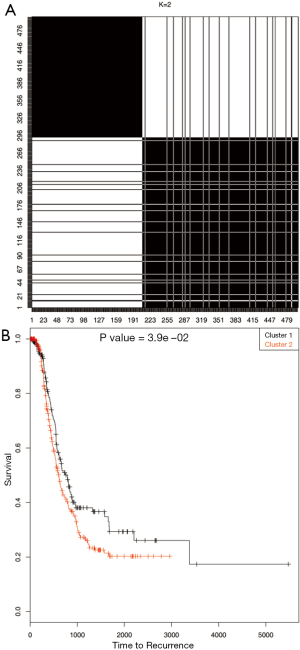
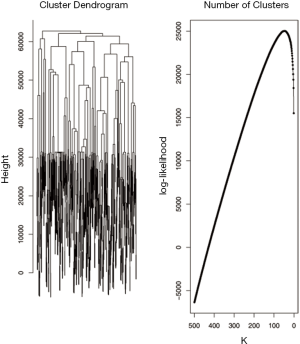
Gene expression data was used to describe the single data clustering methods. For NMF method (15), Matlab software was used and for all other single data clustering methods software R was used. Except in NMF, none of the other single data clustering methods mentioned in the paper has in built method to estimate optimum number of clusters. For NMF method, the plot of cophenetic correlation against number of clusters is used to estimate the number of clusters (Figure 2A). The plot shows that the curve starts bending sharply at k =3 suggesting that three clusters is optimum for this data. To further study the differences in time to recurrence among the identified clusters Kaplan Meier plot followed by the log-rank test of statistical significance was carried out (Figure 2B). The time to recurrence was found significant (P value <3.4×10-11 among the clusters). Next, K-means clustering was carried out using the function kmeans in R. This method requires the analyst to pre-specify the number of clusters. One of the ways to make the initial guess about the number of clusters is by plotting the within groups sums of squares (WSS) against number of clusters (k) (Figure 3A). Generally, it is hard to find the cut-point for the number of clusters looking at the plot (in this example it is hard to say whether it is k =3 or 4). To become consistent with NMF, k =3 was selected for this example and then time to recurrence analysis was carried out as before (Figure 3B). Similarly, the optimum number of clusters selection in hierarchical method is subjective and is based on looking at the dendogram plot. Again in this example it is hard to say how many clusters are appropriate (Figure 4A). For this and the rest of the methods we pre-assign k =3. The resulting clusters from each of the method were further assessed with time to recurrence analyses as mentioned above (Figure 4B). The results and the software functions used to carry out the clustering are summarized in Table 1. Since the time to recurrence plots from all of the methods are similar, to save space, only the plots for NMF, K-means and hierarchical clustering methods are shown in the paper.
Full table
Integrative clustering methods
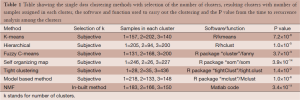
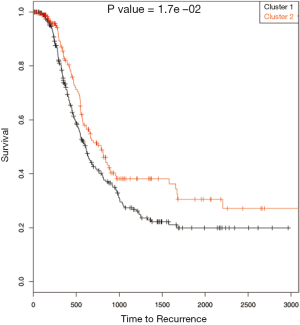
Both the gene expression and methylation data were used for the integrative clustering methods. R functions are available for iCluster and mixture model based clustering methods while Matlab codes are available for integrative clustering based on NMF. The iCluster resulted in optimum number of clusters to be 2. To further study the differences in time to recurrence between the identified clusters Kaplan Meier plot followed by the log-rank test of statistical significance was carried out. The cluster separability plot and Kaplan Meier plot are shown in Figure 5A and Figure 5B respectively. However, the mixture model based clustering method produced large number of clusters (k =48) with our data (Figure 6). One of the reasons this happened could be because the model over fitted the data. Using the cross validation technique (18, pages 214-216) may be helpful in improving the application of the method. Further time to recurrence analyses were not carried out with that result. On the other hand, the purpose of the NMF integrative method mentioned in this paper is to draw the correlated subgroups (MD module) across the samples rather than classifying the samples explicitly into the disjoint clusters. However as suggested by the method, for each MD module, the samples can be classified into two groups: module specific and non-module specific. For our application, we defined k =2 and classified the samples into two groups. Then the two groups were assessed using time to recurrence analyses as mentioned above (Figure 7). The results as well as the software functions used are summarized in Table 2.

Full table
Based on the results it can be inferred that the choice of the method depends on the purpose of the study and nature of the data, whether the data satisfies the model assumptions, only single type of data is available or multiple datasets are available etc. In the absence of the initial number of clusters (which is true in many studies), the method having in-built method of estimating such number would be preferable. In addition, cross validation techniques (the technique in which the data is splitted into two parts, the clustering method is applied in one set of data and the results are validated in other set of data) (18) are recommended to use together with the methods mentioned above in order to make sure that the model is not over fitting the data.
Discussion
Cluster analysis aims to highlight meaningful patterns or groups inherent in the data that will be helpful in identifying the subtypes of the diseases. A reliable and precise classification of diseases is essential in precision medicine. Clinical methods for classification rely on variety of morphological, clinical and molecular variables. However there are uncertainties in diagnosis with such procedures. It is likely that the subtypes thus detected are still heterogeneous in the molecular level and follow the different clinical course. Several types of clustering algorithms have been proposed that use several assays of molecular variation of cells most of which are designed for one type of data at a time. Such methods have been successfully implemented in many disease classification studies. As multiple types of data are increasingly available due to high throughput technologies, an essence of integrative methods of clustering has been more evident and attention has been diverted appreciably towards integrative analysis of clustering. A few attempts have already been made in an effort of developing such methods and have been explained with real data examples. Traditional approach of identifying the subtypes or clusters across the multiple data types is to separately cluster each type of data, followed by manual integration of the results. Manual integration of the results requires great deal of understanding of the biological information but the conclusions drawn will still be subjective. A few comprehensive clustering methods (11-13,52) have also been proposed and successfully implemented in some studies. In this paper, brief review of those methods has been presented.
Integrative clustering methods can also be implemented under three broadly classified statistical learning techniques; unsupervised, supervised and semi-supervised approaches (55,56). The unsupervised method does not use any clinical information about the patient but uses only the genomic data to create subgroups assuming that there exists an unknown mapping that assigns a group “label” to each feature (25) and are based on measuring the similarities between the samples within the defined geometrical distances. A drawback of such methods is that the identified tumor subtypes may not always be correlated to clinical outcomes, such as, survival of the patients, disease status etc. In contrast, supervised method directly focuses the phenotype of interest in order to identify clusters assuming a pre-defined basis of categories. For example, patients can be classified as “high risk” and “low risk” groups based on their survival times (57,58). However, such classification may not necessarily agree with molecular classification. More flexible semi-supervised method combines both the genomic and clinical data sets which involve selecting a list of genomic features that are associated with the clinical variable of interest and then applying unsupervised clustering method to the subset of the data with the pre-selected features (55).
Use of all available genomic information in the determination of clinically relevant molecular subtypes is essential to aid in the detection of novel loci, development of targeted therapies and the understanding of the subsequent biological mechanisms responsible for disease etiology, progression and/or treatment sensitivity/resistance. As such, the role of an efficient statistical method that is able to integrate a disparate number of multiple data types is very important to reach the ultimate goal of improving the ability to understand and predict etiology of complex diseases, such as cancer.
Acknowledgments
Funding: This research was supported by the Department of Biostatistics, University of Kansas Medical Center and funding from National Institute of Health (P20 GM103418; P30 CA168524; R21 CA182715).
Footnote
Provenance and Peer Review: This article was commissioned by the Guest Editors (Dung-Tsa Chen and Yian Ann Chen) for the series “Statistical and Bioinformatics Applications in Biomedical Omics Research” published in Translational Cancer Research. The article has undergone external peer review.
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.3978/j.issn.2218-676X.2014.06.03). The series “Statistical and Bioinformatics Applications in Biomedical Omics Research” was commissioned by the editorial office without any funding or sponsorship. The authors have no other conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Sørlie T, Perou CM, Tibshirani R, et al. Gene expression patterns of breast cancer carcinomas distinguish tumor subclasses with clinical implications. PNAS 2001;98:10869-74. [PubMed]
- Verhaak RG, Hoadley KA, Purdom E, et al. Integrated genomic analysis identifies clinically relevant subtypes of glioblastoma characterized by abnormalities in PDGFRA, IDH1, EGFR, and NF1. Cancer Cell 2010;17:98-110. [PubMed]
- Sotiriou C, Neo SY, McShane LM, et al. Breast Cancer Classification and prognosis based on gene expression profiles from a population-based study. PNAS 2003;100:10393-8. [PubMed]
- Alizadeh AA, Eisen MB, Davis RE, et al. Distinct types of diffuse large B-cell lymphoma identified by gene expression profiling. Nature 2000;403:503-11. [PubMed]
- Lapointe J, Li C, Higgins JP, et al. Gene xpression profiling identifies clinically relevant subtype of prostate cancer. PNAS 2004;101:811-6. [PubMed]
- Eisen MB, Spellman PT, Brown PO, et al. Cluster Analysis and display of genome-wide expression patterns. PNAS 1998;95:14863-8. [PubMed]
- Wirapati P, Sotiriou C, Kunkel S, et al. Meta-Analysis of gene expression profiles in breast cancer: toward a unified understanding of breast cancer subtyping and prognosis signature. Breast Cancer Res 2008;10:R65. [PubMed]
- Ang PW, Loh M, Liem N, et al. Comprehensive profiling of DNA methylation in colorectal cancer reveals subgroups with distinct clinicopathological and molecular features. BMC Cancer 2010;10:227. [PubMed]
- Marsit CJ, Christensen BC, Houseman EA, et al. Epigenetic profiling reveals etiologically distinct patterns of DNA methylation in head and neck squamous cell carcinoma. Carcinogenesis 2009;30:416-22. [PubMed]
- Issa JP. CpG island methylator phenotype in cancer. Nat Rev Cancer 2004;4:988-93. [PubMed]
- Shen R, Olshen AB, Ladanyi M. Integrative clustering of multiple genomic data types using a joint latent variable model with application to breast cancer subtype analysis. Bioinformatics 2009;25:2906-12. [PubMed]
- Zhang S, Liu CC, Li W, et al. Discovery of multi-dimensional modules by integrative analysis of cancer genomic data. Nucleic Acids Res 2012;40:9379-91. [PubMed]
- Kormaksson M, Booth JG, Figueroa ME, et al. Integrative Model-based Clustering of microarray methylation and expression data. Ann Appl Stat 2012;6:1327-47.
- Tibshirani R, Hastie T, Narashimhan B, et al. Diagnosis of Multiple Cancer types by Shrunken Centroids of Gene Expression. PNAS 2002;99:6567-72. [PubMed]
- Brunet JP, Tamayo P, Golub TR, et al. Metagenes and molecular pattern discovery using matrix factorization. Proc Natl Acad Sci U S A 2004;101:4164-9. [PubMed]
- Koestler DC, Marsit CJ, Christensen BC, et al. Semi-supervised recursively partitioned mixture models for identifying cancer subtypes. Bioinformatics 2010;26:2578-85. [PubMed]
- Handl J, Knowles J, Kell DB. Computational Cluster Validation in post-genomic data analysis. Bioinformatics 2005;21:3201-12. [PubMed]
- Hastie T, Tibshirani R, Friedman J. eds. The Elements of Statistical Learning: Data Mining, Inference and Prediction. New York: Springer, 2001.
- Tavazoie S, Hughes JD, Campbell MJ, et al. Systematic determination of genetic architecture. Nat Genet 1999;22:281-5. [PubMed]
- Kim EY, Kim SY, Ashlock D, et al. MULTI-K: accurate classification of microarray subtypes using ensemble k-means clustering. BMC Bioinformatics 2009;10:260. [PubMed]
- Kaufman L, Rousseeuw PJ. eds. Finding groups in data: An Introduction to Cluster Analysis. New Jersey: John Wiley & Sons, 1990.
- Bhattacharjee A, Richards WG, Staunton J, et al. Classification of Human lung carcinomas by mRNA expression profiling reveals distinct adenocarcinoma subclasses. PNAS 2001;98:13790-5. [PubMed]
- Beer DG, Kardia SL, Huang CC, et al. Gene-expression profiles predict survival of patients with lung adenocarcinoma. Nat Med 2002;8:816-24. [PubMed]
- Sherlock G. Analysis of large-scale gene expression data. Curr Opin Immunol 2000;12:201-5. [PubMed]
- Kerr G, Ruskin HJ, Crane M, et al. Techniques for clustering gene expression data. Comput Biol Med 2008;38:283-93. [PubMed]
- Bezdek JC. eds. Pattern Recognition with Fuzzy Objective Function Algorithms. New York: Springer, 1981.
- Dembélé D, Kastner P. Fuzzy C-means method for clustering microarray data. Bioinformatics 2003;19:973-80. [PubMed]
- Tari L, Baral C, Kim S. Fuzzy c-means clustering with prior biological knowledge. J Biomed Inform 2009;42:74-81. [PubMed]
- Kohonen T. The Self-organizing Map. Proc IEEE Conf 1990;78:1464-80.
- Kohonen T. eds. Self-Organizing Maps. Berlin: Springer, 2001.
- Tamayo P, Slomin D, Mesirov J, et al. Interpreting patterns of gene expression with self-organizing maps: Methods and application to hematopoietic differentiation. PNAS 1999;96:2907-12. [PubMed]
- Torkkola K, Gardner RM, Kaysser-Kranich T, et al. Self-Organizing maps in mining gene expression data. Information Sciences 2001;139:79-96.
- Nikkilä J, Törönen P, Kaski S, et al. Analysis and Visualization of gene expression data using Self-Organizing Maps. Neural Networks 2002;15:953-66. [PubMed]
- Patterson AD, Li H, Eichler GS, et al. UPLC-ESI-TOFMS-Based Metabolomics and Gene Expression Dynamics Inspector Self-Organizing Metabolomic Maps as Tools for Understanding the Cellular Response to Ionizing Radiation. Anal Chem 2008;80:665-74. [PubMed]
- Tseng GC, Wong WH. Tight clustering: A resampling based approach for identifying stable and tight patterns in the data. Biometrics 2005;61:10-6. [PubMed]
- Tseng GC. A Comparative Review of Gene Clustering in Expression Profile. Proc 8th International Conference on Control, Automation, Robotics and Vision (ICARCV) 2004;2:1320-4.
- Fraley C, Raftery AE. How many clusters? Which cluster method? Answer via model based cluster analysis. Computer J 1998;41:578-88.
- Pan W, Lin J, Le CT. Model based cluster analysis of microarray gene-expression data. Genome Biol 2002;3:RESEARCH0009.
- McLachlan GJ, Bean RW, Peel D. A mixture model based approach to the clustering of microarray expression data. Bioinformatics 2002;18:413-22. [PubMed]
- McNicholas PD, Murphy TB. Model-based clustering of microarray expression data via latent Gaussian Mixture models. Bioinformatics 2010;26:2705-12. [PubMed]
- Yeung KY, Fraley C, Murua A, et al. Model based clustering and data transformations for gene expression data. Bioinformatics 2001;17:977-87. [PubMed]
- Schwartz G. Estimating the dimension of a model. Ann Stat 1978;6:461-4.
- Paatero P, Tapper U. Positive Matrix factorization: A non-negative factor model with optimal utilization of error estimates of data values. Environmerics 1994;5:111-26.
- Lee DD, Seung HS. Learning the parts of objects by non-negative matrix factorization. Nature 1999;401:788-91. [PubMed]
- Kim PM, Tidor B. Subsystem identification through dimensionality reduction of large scale gene expression data. Genome Res 2003;13:1706-18. [PubMed]
- Liu W, Yuan K, Ye D. Reducing microarray data via non-negative matrix factorization for visualization and clustering analysis. J Biomed Inform 2008;41:602-6. [PubMed]
- Monti S, Tamayo P, Mesirov J, et al. Consesus Clustering: A resampling based method for class discovery and visualization of gene expression microarray data. Machine Learning 2003;52:91-118.
- Tipping ME, Bishop CM. Probabilistic Principal Component Analysis. J Royal Statistical Society 1999;61:611-22.
- Zha H, He X, Ding C, et al. Spectral Relaxation for K-means clustering. Available online: http://ranger.uta.edu/~chqding/papers/KmeansNIPS2001.pdf
- Dempster AP, Laird NM, Rubin DB. Maximum Likelihood from Incomplete Data via The EM Algorithm (with discussion). Journal of the Royal Statistical Society 1977;39:1-38.
- Tibshirani R. Regression Shrinkage and Selection via the Lasso. Journal of the Royal Statistical Society 1996;58:267-88.
- Shen R, Wang S, Mo Q. Sparse Integrative clustering of multiple omics data sets. Ann Appl Stat 2013;7:269-94. [PubMed]
- Zou H, Hastie T. Regularization and variable selection via the Elastic Net. J Royal Statistical Society 2005;67:301-20.
- Tibshirani R, Saunders M, Rosset S, et al. Sparsity and smoothness via the fused lasso. J Royal Statistical Society 2005;67:91-108.
- Bair E, Tibshirani R. Semi-Supervised Methods to Predict Patient Survival from Gene Expression Data. PLoS Biology 2004;2:E108 [PubMed]
- Hastie T, Tibshirani R, Friedman J. eds. The Elements of Statistical Learning: Data Mining, inference and Prediction. New York: Springer, 2001.
- Shipp MA, Ross KN, Tamayo P, et al. Diffuse large cell lymphoma outcome prediction by gene-expression profiling and supervised machine learning. Nature Medicine 2002;8:68-74. [PubMed]
- Marcel D, Bühlmann P. Supervised clustering of genes. Genome Biol 2002;3:RESEARCH0069.


