Identification of cancer mechanisms through computational systems modeling

Introduction

Colorectal cancer is characterized by uncontrolled cell growth in the colon or rectum. About 140,000 people were diagnosed with colorectal cancer, and almost 50,000 people died of the disease in 2011, in the US alone (1). Based on rates from 2007-2009, 5% of US men and women born today are expected to be diagnosed with colorectal cancer during their lifetimes (2). Worldwide, colorectal cancer is among the top three causes of cancer in both women and men (3), and, together with lung, stomach, and liver cancer, is the most common cause of cancer death.

Colorectal cancer has been extensively investigated in the laboratory and the clinics. Due to available technologies, most of this research has focused on genetic and epigenetic aspects. Interestingly, the average colorectal cancer case exhibits only one or two oncogene mutations, which are typically accompanied by several tumor suppressor mutations; by contrast, epigenetic alterations are quite frequent (4). This finding is important because a single epigenetic event can cause alterations in the expression of hundreds of genes. In particular, methylation of microRNA genes can alter the expression of these non-coding sequences and secondarily change the expression of many protein-coding genes that are their targets. An example for such a microRNA is miR-137, whose CpG island methylation occurs early in the majority of colorectal cancer cases and alters the expression of about 500 target genes (5). This fact raises important biological questions, such as the following. Are changes in each one of these 500 target genes significantly related to the onset and/or progression of carcinoma? Which apparently affected genes are critical? Answering these questions will not only help us gain deeper insights into the molecular mechanisms of cancer, but might also facilitate the development of targeted diagnoses or medications for colorectal cancer.

Various high-throughput “-omics” datasets have been generated over the past decade and are very useful for seeking possible answers to the above questions. Among these -omics data, metabolomics profiles are especially useful because they can be used to connect actual function, as seen in changes in metabolites, with molecular mechanism in the form of changes in enzymatic activities. This connection is implicitly buried within the data and can hardly be extracted with intuition or laboratory experiments. However, it can be inferred to some degree with computational methods, which are proposed here.

We apply such an approach to colorectal carcinoma, using mathematical and computational methods, which we have detailed elsewhere in a different context (6). We focus particularly on purine metabolism, because it generates nucleotides that cancer cells require in large amounts (7-9). As Otto Warburg noticed as early as 1926 (10,11), cancer relies on altered cellular metabolism for its uncontrolled cellular growth.

For colorectal cancer, various metabolomics platforms have been developed; they include nuclear magnetic resonance, gas-chromatographic mass spectrometry, liquid chromatography mass spectrometry, capillary electrophoresis mass spectrometry, Fourier transform ion cyclotron resonance mass spectrometry, and ion mobility mass spectrometry. As a consequence, dozens of metabolomics datasets for colorectal cancer have been generated in recent years. These datasets contain enormous information, which however is implicit and must be extracted with computational means.

To discover alterations in enzyme activities that can potentially effect the observed changes in a metabolomics profile, a customized modeling framework is required that includes both enzymes and metabolites as its components and allows the inference of one from the other. Almost by necessity, such a modeling framework must be a dynamical model of a metabolic pathway in the format of ordinary differential equations (ODEs). Here, we employ such a model (12) to investigate purine metabolism, which exhibits increased activity in colorectal carcinoma, as it provides ribonucleotides and deoxyribonucleotides that are urgently needed for cell proliferation. With metabolomics data as input and such a mathematical model as a computational platform, it is indeed possible to identify sets of enzymes that can cause observed changes in metabolic profile, if their activities are altered. In this study, we apply such an approach to study colorectal carcinoma cases.

Methods

To infer molecular mechanisms of colorectal carcinoma, we need suitable metabolomics data from normal and tumor tissues, a mathematical model of purine metabolism, and a customized computational method. We describe these components in the following sections.

Metabolomics data

Metabolomics data for colorectal carcinoma were obtained by Hirayama et al. (8), who sampled tumor and surrounding normal tissues from 16 colorectal carcinoma patients. Metabolites in these samples were analyzed and measured with capillary electrophoresis time-of-flight mass spectrometry. Here we focus on data associated with purine metabolism; they are summarized in Table 1. As one might expect, not all metabolites in the purine pathway were measured, and not all measured metabolites showed statistically significant alterations in tumor samples compared to normal samples. Hirayama’s experimental data are used here for the inference of molecular mechanisms in this study.

Table 1 Metabolomics data relevant to purine metabolism for colorectal cancer^%
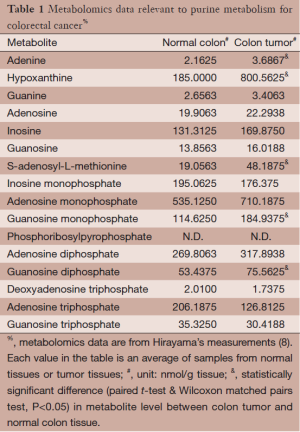
Full table

Mathematical model of purine metabolism

Purine metabolism constitutes a complex and highly regulated pathway system (Figure 1). Among other products, it is the main source for purine nucleotides that are needed for DNA and RNA synthesis. Due to its central importance, deficits in purine metabolism are associated with a number of human diseases, including cancer.

Figure 1 Human purine metabolism. Human purine metabolism constitutes a very important and complex metabolic pathway. It contains a de novo synthesis pathway (red arrows) and salvage pathways (green arrows) for purine bases. Reactions are represented with arrows. Metabolites are shown in dashed boxes and enzymes are annotated as italic EC numbers. Table 2 lists enzyme names and their abbreviations. The map is adapted from Curto’s work (12-14). Regulations are omitted for a clearer visualization. PRPP, phosphoribosylpyrophosphate; IMP, inosine monophosphate; S-AMP, adenylosuccinate; Ado, adenosine; AMP, adenosine monophosphate; ADP, adenosine diphosphate; ATP, adenosine triphosphate; SAM, S-adenosyl-L-methionine; Ade, adenine; XMP, xanthosine monophosphate; GMP, guanosine monophosphate; GDP, guanosine diphosphate; GTP, guanosine triphosphate; dAdo, deoxyadenosine; dAMP, deoxyadenosine monophosphate; dADP, deoxyadenosine diphosphate; dATP, deoxyadenosine triphosphate; dGMP, deoxyguanosine monophosphate; dGDP, deoxyguanosine diphosphate; dGTP, deoxyguanosine triphosphate; RNA, ribonucleic acid; DNA, deoxyribonucleic acid; HX, hypoxanthine; Ino, inosine; dIno, deoxyinosine; Xa, xanthine; Gua, guanine; Guo, guanosine; dGuo, deoxyguanosine; UA, uric acid; R5P, ribose-5-phosphate.

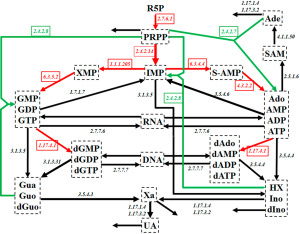
As Figure 1 shows, the system contains a main de novo synthesis route, as well as salvage pathways for recycling purine bases. The de novo synthesis begins with ribose-5-phosphate (R5P) and involves several enzymatic steps, which are collectively shown as red arrows in Figure 1. As an alternative, purine bases can be recycled through a salvage pathway (green arrows in Figure 1). Uric acid (UA), xanthine (Xa), hypoxanthine (HX), adenine (Ade), and some other metabolites leave the system.

Curto and coworkers developed a mathematical model of human purine metabolism [(12-14), see also (15)]. This model consists of a system of ODEs with 16 dependent variables and 37 fluxes, expressed in the format of Biochemcial Systems Theory [e.g., (15-20)]. R5P and P_i are treated as independent variables and are thus not changed during model simulations. Curto’s results showed that the system can tolerate quite large changes in metabolite levels and still return to its steady state. With a low sensitivity profile, the system is also structurally robust. Curto’s dynamical model is used here directly, and without changes (14).

Computational inference approach

The proposed approach uses the mathematical model of purine metabolism and Hirayama’s metabolomics data for colorectal carcinoma as input, and applies a multi-step strategy to narrow down reaction steps likely to be affected by cancer. While technical details were described in a recent report focusing on a different context (6), it is necessary for understanding the following that we review the core concepts of the method.

Using model simulations, it is easy to alter enzyme activities one by one, or many, or all of them simultaneously, and to assess how the perturbation changes the metabolite levels at the steady state. Because this procedure is straightforward, it permits large-scale repetitions of this type of assessment in the form of Monte-Carlo simulations. We executed millions of such simulations, each time varying the perturbations. As a consequence, statistically robust conclusions are reached instead of just a single outcome.

Specifically, we implemented the approach as a three-step strategy. The purpose of the 1^st step is to reduce the number of candidate sites targeted by colorectal cancer with consideration of only qualitative information, namely the direction (increase or decrease) in the resultant changes in metabolites at the steady state. We first allowed all enzymes and reaction rates of non-enzymatic reactions to change simultaneously, and compared the simulation results with the reported metabolomics data. Out of millions of simulations, we retained only those that showed the same type of change (increased or decreased) in significantly altered metabolites from their nominal levels as observed in the tumor tissues, according to the metabolomics data. After many simulations, the values of each parameter in the sets surviving this filtering form a frequency distribution. A non-skewed distribution (uniform, Gaussian, or otherwise symmetric) suggests that the parameter is not likely affected by the tumor, because higher or lower values are similarly found in the filtered solutions. By contrast, if the observed profile is only reachable if a certain parameter value is (essentially) always increased or (essentially) always decreased, some unknown constraints are presumably in effect that reject cases pointing in the opposite direction. Using this criterion of distributional skewness reduces the number of candidate parameters immensely. Only parameters surviving this first filtering step are considered further.

For step 2, we use quantitative concentration values from the metabolomics data. This criterion is different from the qualitative criterion for the 1^st step and much more stringent. Specifically, we consider only parameters remaining from the initial filtering, alter these through further Monte-Carlo simulations, and calculate the difference between each simulation result and the metabolomics data in terms of relative changes in metabolites levels. We determine the overall fitness of a simulation result with respect to metabolomics data as the 2-dimensional Euclidean norm of their differences and select one thousand sets of parameter values with the best fitness values out of one million simulations for the next step. Thus, the main purpose of the 2^nd step is to shrink the space of feasible parameter values.

The selected top one thousand sets of parameter values enter into the 3^rd step. They are used as initial parameter values for an optimization procedure based on a genetic algorithm. This optimization procedure generates a new set of parameter values with even better fitness than those sets from step 2. Among these, we select a subset of parameter values that make the model system fit the recorded data best. Finally, we generate distributions of parameter values from this subset and analyze the skewness for each parameter. This step is designed to identify the most likely sites affected by cancer. Not only the locations of the targeted sites can be inferred in this manner, but also the intensity of the effect at a site can be derived.

Results

In accordance with the three steps of the approach described in the Methods section, the results are divided into three parts.

Step 1

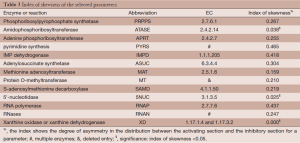
Out of five million Monte Carlo simulations, we only retained those results that showed same direction of significant change (positive, increased; negative, decreased) as the observed changes in tumor tissues. This qualitative filtering resulted in an enormous reduction (almost 95%) from all initially simulated parameter sets (5,000,000 sets) into a much smaller feasible subpopulation (287,473 sets). For each model parameter in the latter sets, we generated a distribution of its values (Figure 2). These distributions allowed us to calculate their skewness coefficients. Parameters with essentially symmetric distributions (uniform, Gaussian, etc.) were excluded from further considerations. Table 2 shows the list of likely and unlikely target sites. The 13 parameters passing the filtering are associated with: phosphoribosylpyrophosphate synthetase (PRPPS) (P1), amidophosphoribosyltransferase (ATASE) (P2), adenine phosphoribosyltransferase (APRT) (P4), pyrimidine synthesis (PYRS) (P5), inosine monophosphate dehydrogenase (IMPD) (P6), adenylosuccinate synthetase (ASUC) (P8), methionine adenosyltransferase (P12), protein O-methyltransferase (MT) (P13), S-adenosylmethionine decarboxylase (SAMD) (P14), 5'-nucleotidase (5NUC) (P15), RNA polymerase (RNAP) (P19), RNases (RNAN) (P20), and xanthine oxidase/dehydrogenase (XD) (P23). These 13 parameters were retained for the next step, while the remaining 14 parameters were henceforth excluded.

Figure 2 Distributions of values from the selected subpopulation parameter sets. Only simulation results were kept that show the same sign of change (+, increased; –, decreased) in significantly altered metabolites (in comparison with their nominal levels) as the changes in tumor tissues identified by metabolomics methods (8). Out of five million initial Monte Carlo simulations, a relatively small subpopulation (287,473 sets) was selected. X-axes are fold changes in parameter values with respect to their nominal levels. The parameters are associated with the following reaction steps: P1, phosphoribosylpyrophosphate synthetase; P2, amidophosphoribosyltransferase; P3, hypoxanthine-guanine phosphoribosyltransferase; P4, adenine phosphoribosyltransferase; P5, pyrimidine synthesis; P6, inosine monophosphate dehydrogenase; P7, guanosine monophosphate synthetase; P8, adenylosuccinate synthetase; P9, adenylosuccinate lyase; P10, guanosine monophosphate reductase; P11, adenosine monophosphate deaminase; P12, methionine adenosyltransferase; P13, protein O-methyltransferase; P14, S-adenosylmethionine decarboxylase; P15, 5'-nucleotidase; P16, 5'(3') nucleotidase; P17, diribonucleotide reductase; P18, adenosine deaminase; P19, RNA polymerase; P20, RNAses; P21, DNA polymerase; P22, DNAses; P23, xanthine oxidase/xanthine dehydrogenase; P24, guanine hydrolase; P25, hypoxanthine excretion; P26, xanthine excretion; P27, uric acid excretion.

Table 2 Parameters are screened out based on five million Monte Carlo simulations
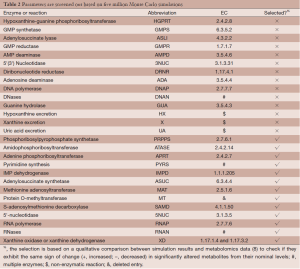
Full table

Step 2

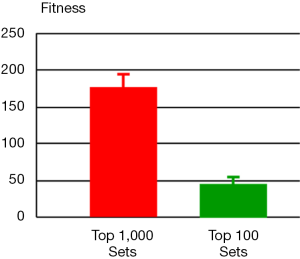
For the 2^nd step, we ran one million simulations with perturbations affecting only the selected 13 parameters from step 1. For each simulation result, we computed its fitness with respect to the metabolomics data that exhibit alterations of metabolite levels in tumor tissues versus normal tissues. The resulting one million sets of parameter values were sorted according to their fitness in ascending order. The top one thousand sets were selected and entered into the 3^rd step (Figure 3). The distribution of fitness values from these selected parameter sets has a mean value of 175.7 (±19.2), which is in stark contrast to the value for the entire one million parameter sets: 1,771.4 (±3,618.1). Thus, this step of using quantitative information shrinks the space of parameter values enormously.

Figure 3 Fitness of selected sets of parameter values. The original set (in red) contains the top one thousand sets of parameter values selected from the 2^nd step, which shows a mean fitness of 175.7 (±19.2). The optimized set (in green) represents the top one hundred parameter sets after an optimization procedure and has an overall improved fitness of 46.5±7.7.

Step 3

An optimization procedure was run on the selected top one thousand parameter sets from the 2^nd step. Specifically, the values of these parameters were used as the initial values for a genetic algorithm that generated one thousand fine-tuned parameter sets with improved fitness. The distribution of fitness values from the optimized parameter sets has a mean value of 126.9 (±209.3), which shows an overall improvement of fitness but spreads much wider than the original one thousand parameter sets. Among the optimized parameter sets, we chose the top one hundred sets with the best fitness (46.5±7.7, Figure 3) and calculated a skewness coefficient for each parameter (Table 3). The results suggest that just three enzymes emerge as most likely targets of colorectal carcinoma, namely: ATASE, 5NUC, and XD. The intensities of alterations, expressed as fold changes with respect to their nominal values, in cancer as opposed to normal tissue, at these sites were inferred as: 2.337 (activation), 0.673 (inhibition), and 0.349 (inhibition), respectively.

Table 3 Index of skewness of the selected parameters
Full table

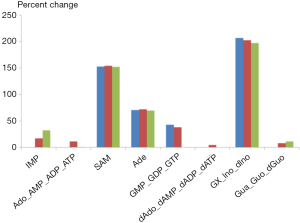
As an illustration, we selected the first and last ranking parameter sets (1^st and 100^th) from the optimized one hundred sets and implemented them into the purine model. Figure 4 shows the simulated alterations of metabolites levels in tumor tissue and their comparisons with metabolomics data. Indeed, both parameter sets trigger comparable changes within the metabolites of the purine system, and these changes are very similar to the metabolic profile observed in colorectal carcinoma using capillary electrophoresis time-of-flight mass spectrometry.

Figure 4 Simulated alterations of metabolites levels in tumor tissues and their comparison with metabolomics data. The X-axis represents eight metabolites of the purine system, for which metabolomics data are available. For each metabolite, three bars are shown: blue for metabolomics measurements from capillary electrophoresis time-of-flight mass spectrometry, red for 1^st set of the optimized one hundred parameter sets, and green for the 100^th set of the optimized one hundred parameter sets. Some metabolites with no significant changes in the metabolomics data are close to zero and therefore not visible. As shown, these two representative parameter sets exhibit changes within the purine system in terms of the metabolic profile that are comparable to those observed in colorectal carcinoma (8). IMP, inosine monophosphate; Ado, adenosine; AMP, adenosine monophosphate; ADP, adenosine diphosphate; ATP, adenosine triphosphate; SAM, S-adenosyl-L-methionine; Ade, adenine; GMP, guanosine monophosphate; GDP, guanosine diphosphate; GTP, guanosine triphosphate; dAdo, deoxyadenosine; dAMP, deoxyadenosine monophosphate; dADP, deoxyadenosine diphosphate; dATP, deoxyadenosine triphosphate; HX, hypoxanthine; Ino, inosine; dIno, deoxyinosine; Gua, guanine; Guo, guanosine; dGuo, deoxyguanosine.

Conclusions and discussion

Many metabolomics studies of different types of cancers have been performed in recent times with different experimental platforms (7-9,21-26). Compared to other -omics high-throughput data, these metabolomics data have the unique advantage that they can be used to connect function, in the form of metabolites, with molecular mechanisms or strategies in the form of altered enzyme activities. This connection is initially not explicit, but we have shown here that it can be extracted from the metabolomics data, if a dynamic mathematical model and a customized computational inference strategy are available.

Here, we used this combined approach of systems biology to infer the molecular strategy with which colorectal carcinoma appears to modulate purine metabolism in order to increase the availability of nucleotides, which are required for cancer growth. Our combined approach provides a statistically robust conclusion. It seems difficult to imagine an experimental approach that could have revealed such a strategy.

Our approach initially allowed all processes within purine metabolism to be potential targets of colorectal cancer, but quickly narrowed down the domain of candidate targets and ultimately identified, in a statistically significant and robust fashion, three enzymes as most likely affected sites. These three enzymes are: amidophosphoribosyltransferase ATASE (EC: 2.4.2.14), which is considered the first committed and rate limiting step of de novo purine biosynthesis; 5'-nucleotidase (EC: 3.1.3.5), which catalyzes inosine monophosphate (IMP) to inosine (Ino) and guanosine monophosphate (GMP) to guanosine (Guo); and XD (EC: 1.17.3.2 and 1.17.1.4), which catalyzes HX to Xa and then to UA, as well as the oxidation of Ade to 2,8-dihydroxyadenine and the excretion of them into urine.

Among these three predicted targets, the activity of ATASE (EC: 2.4.2.14) is predicted to be elevated more than 2-fold in colorectal carcinoma (mean fold change: 2.337±1.275). This result is easily interpreted as a higher activity increases the overall availability of purines. By contrast, the activity of 5NUC is reduced to two thirds (mean fold change: 0.673±0.195) of its normal level. This enzyme removes material from central purine metabolism to Ino and HX, from where much of it is oxidized to Xa. Thus, this enzyme siphons substrate away from nucleotide production. Similarly, the same enzyme removes phosphorylated guanosine, in direct competition with incorporation into RNA or DNA. Finally, the model analysis indicates that xanthine oxidase (XO) is reduced to one third of its normal activity (mean fold change: 0.349±0.110). This enzyme competes with the enzyme hypoxanthine-guanine phosphoribosyltransferase [(HGPRT), EC: 2.4.2.8] for the substrate HX and excretes the substrate Ade for the enzyme APRT (EC: 2.4.2.7). Both enzymes are associated with the salvage of purine metabolism. HGPRT recycles material back to IMP, the center of purine metabolism. The flux through this process is increased if the activity of XO is strongly reduced. Expressed differently, a reduction in XO activity, as it is inferred here, increases the recycling of material toward added nucleotide production through the salvage pathway. Similarly, the dehydrogenase (EC: 1.17.1.4) removes Ade irreversibly from the system instead of allowing it to return to the pool of adenosine and its phosphorylated forms. Thus, the purely computational model inferences, which were obtained without any bias by formerly infused information, interpretation or speculation, reveal three key processes for the increased production of nucleotides, which in retrospect are easy to explain, but were not necessarily easy to predict.

Although the inferred significance of changes in these three enzymes is clear, our analysis suggests that changes in the three enzymes alone do not fully explain the observed metabolic alterations of the purine system in colorectal carcinoma. In addition to their modulations, about ten other enzyme activities appear to be altered. While these changes are of a much lesser degree, the affected secondary action sites are still of potential interest and deserve further study. At any rate, the inferences render it clear that it is not a single change that resets the normal metabolic profile in cancer, but that enzyme activity alterations are distributed among three main and ten secondary drivers.

The molecular mechanisms inferred in this study for colorectal carcinoma suggest functional, mechanistic connections between perturbed genes and proteins on the one hand and an altered profile of purine metabolites on the other. These predictions suggest specific research foci for biologists and clinicians interested in investigating the biochemical mechanisms leading to metabolic perturbations in colorectal cancer. More generally, the study improves our understanding of the pathology of the disease, and may thus aid in potentially better diagnoses and treatments. Intriguingly, the findings pose the question of whether it might be possible to counteract the alterations with subtle, but targeted drug treatments that could affect the primary and/or secondary action sites revealed here and thereby return the purine system to a close resemblance of normalcy.

Acknowledgments

Funding: This work was supported by a grant from the National Institutes of Health (P01-ES016731, Gary W. Miller, PI), a contract from NIH/NIAID (HHSN272201200031C; Mary Galinsky, PI), and an endowment from the Georgia Research Alliance (EOV, PI). Any opinions, findings, conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the sponsoring institutions.

Footnote

Provenance and Peer Review: This article was commissioned by the Guest Editors (Dung-Tsa Chen and Yian Ann Chen) for the series “Statistical and Bioinformatics Applications in Biomedical Omics Research” published in Translational Cancer Research. The article has undergone external peer review.

Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.3978/j.issn.2218-676X.2014.05.03). The series “Statistical and Bioinformatics Applications in Biomedical Omics Research” was commissioned by the editorial office without any funding or sponsorship. The authors have no other conflicts of interest to declare.

Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). In this study we only used data published in the literature. Institutional approval was therefore not needed and informed consent was waived.

Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.

References

1. American Cancer Society. Colorectal Cancer Facts & Figures 2011-2013. Atlanta: American Cancer Society, 2011.
2. Howlader N, Noone AM, Krapcho M, et al. eds. SEER Cancer Statistics Review, 1975-2009 (Vintage 2009 Populations). Bethesda, MD: National Cancer Institute, 2012.
3. Jemal A, Bray F, Center MM, et al. CA Cancer J Clin 2011;61:69-90. [PubMed]
4. Vogelstein B, Papadopoulos N, Velculescu VE, et al. Cancer genome landscapes. Science 2013;339:1546-58. [PubMed]
5. Balaguer F, Link A, Lozano JJ, et al. Epigenetic silencing of miR-137 is an early event in colorectal carcinogenesis. Cancer Res 2010;70:6609-18. [PubMed]
6. Qi Z, Miller GW, Voit EO. Rotenone and paraquat perturb dopamine metabolism: A computational analysis of pesticide toxicity. Toxicology 2014;315:92-101. [PubMed]
7. Denkert C, Budczies J, Weichert W, et al. Metabolite profiling of human colon carcinoma--deregulation of TCA cycle and amino acid turnover. Mol Cancer 2008;7:72. [PubMed]
8. Hirayama A, Kami K, Sugimoto M, et al. Quantitative metabolome profiling of colon and stomach cancer microenvironment by capillary electrophoresis time-of-flight mass spectrometry. Cancer Res 2009;69:4918-25. [PubMed]
9. Ong ES, Zou L, Li S, et al. Metabolic profiling in colorectal cancer reveals signature metabolic shifts during tumorigenesis. Mol Cell Proteomics 2010; [PubMed]
10. Levine AJ, Puzio-Kuter AM. The control of the metabolic switch in cancers by oncogenes and tumor suppressor genes. Science 2010;330:1340-4. [PubMed]
11. Warburg O, Wind F, Negelein E. The metabolism of tumors in the body. J Gen Physiol 1927;8:519-30. [PubMed]
12. Curto R, Voit EO, Sorribas A, et al. Mathematical models of purine metabolism in man. Math Biosci 1998;151:1-49. [PubMed]
13. Curto R, Voit EO, Cascante M. Analysis of abnormalities in purine metabolism leading to gout and to neurological dysfunctions in man. Biochem J 1998;329:477-87. [PubMed]
14. Curto R, Voit EO, Sorribas A, et al. Validation and steady-state analysis of a power-law model of purine metabolism in man. Biochem J 1997;324:761-75. [PubMed]
15. Voit EO. eds. Computational analysis of biochemical systems: a practical guide for biochemists and molecular biologists. Cambridge: Cambridge University Press, 2000.
16. Savageau MA. Biochemical Systems Analysis: A Study of Function and Design in Molecular Biology. Reading, Mass: Addison-Wesley Pub Co Advanced Book Program (reprinted 2009), 1976.
17. Sims KJ, Alvarez-Vasquez F, Voit EO, et al. A guide to biochemical systems modeling of sphingolipids for the biochemist. Methods Enzymol 2007;432:319-50. [PubMed]
18. Torres NV, Voit EO. Pathway Analysis and Optimization in Metabolic Engineering. Cambridge: Cambridge University Press, 2002.
19. Voit EO. A First Course in Systems Biology. New York: Garland Science, 2012.
20. Voit EO. Biochemical Systems Theory (BST): A review. International Scholarly Research Network (ISRN) - Biomathematics, 2013:1-53.
21. Cheng Y, Xie G, Chen T, et al. Distinct urinary metabolic profile of human colorectal cancer. J Proteome Res 2012;11:1354-63. [PubMed]
22. Gong Y, Wang N, Wu F, et al. Proteome profile of human breast cancer tissue generated by LC-ESI-MS/MS combined with sequential protein precipitation and solubilization. J Proteome Res 2008;7:3583-90. [PubMed]
23. Mal M, Koh PK, Cheah PY, et al. Development and validation of a gas chromatography/mass spectrometry method for the metabolic profiling of human colon tissue. Rapid Commun Mass Spectrom 2009;23:487-94. [PubMed]
24. Righi V, Durante C, Cocchi M, et al. Discrimination of healthy and neoplastic human colon tissues by ex vivo HR-MAS NMR spectroscopy and chemometric analyses. J Proteome Res 2009;8:1859-69. [PubMed]
25. Toyama A, Nakagawa H, Matsuda K, et al. Deglycosylation and label-free quantitative LC-MALDI MS applied to efficient serum biomarker discovery of lung cancer. Proteome Sci 2011;9:18. [PubMed]
26. Zeng X, Hood BL, Zhao T, et al. Lung cancer serum biomarker discovery using label-free liquid chromatography-tandem mass spectrometry. J Thorac Oncol 2011;6:725-34. [PubMed]