Applications of imaging processing to MRgFUS treatment for fibroids: a review
Introduction
Uterine fibroids is a very common pathology in females and typically found during the middle and later reproductive years (1,2). Depending on the severity of the symptoms, there are different approaches to treat uterine fibroids: (I) medication; (II) surgically-aided methods; (III) myomectomy; and (IV) hysterectomy (3).
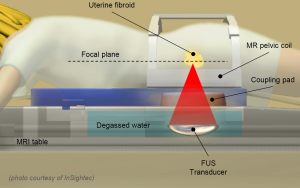
Magnetic resonance guided focused ultrasound (MRgFUS) is an innovative and non-invasive technology based on the use of focused ultrasound (Figure 1) for the thermal ablation of various types of lesions and diseases (4-8). Compared to highly invasive surgical approaches for uterine fibroids treatment, MRgFUS is a safe and effective technique, not aggressive for the patient, by helping to save the surrounding healthy tissues and, thus, to keep the woman’s reproductive potential (9-11). The non-invasiveness of the MRgFUS technique makes it possible to minimize risks and complications, not requiring hospitalization and allowing patients to return to their normal activities in only a few days.
In MRgFUS treatments, MR image analysis is required in fibroids diagnosis, in the subsequent treatment phases, and in the patient follow-up. In the pre-treatment stage, some regions of interest (ROI) must be identified by the selection of some control points needed (I) for machine calibration (InSightec ExAblate 2100 integrated with the MR scanner GE Signa HTxt); (II) for treatment planning; and (III) for the localization (with fiducial markers) of the uterus/fibroids and of the neighbouring organs to protect from ultrasound. In a post-treatment phase segmentation is used to estimate the non perfused volume (NPV), the fibroids area ablated with ultrasound.
The particular characteristic that allows MRgFUS to differentiate from others based on focused ultrasound, is the on-line use of MR images for the identification/selection of the ROI to be treated, as well as for thermal monitoring of ablated areas, using proton resonance shift (PRF) thermometry principles.
Open issues in MRgFUS treatment
In MRgFUS treatment procedures it is possible to identify some open issues that should be addressed to improve the efficacy and efficiency of the treatment: efficacy in terms of enhancement of therapeutic results, efficiency on the basis of the time required by the machine for treatment completion.
Nowadays, uterus/fibroids segmentation is performed manually through time-consuming and operator-dependent procedures. Operator dependence is a critical issue in terms of result reproducibility, while the length of time for treatment planning represents a problem because the patient must stand still during the MRgFUS procedure and the healthcare operator is busy. In addition to these problems, closely linked to the identification of the ROIs (both in the pre-and the post-treatment phases), the continuous monitoring of the temperature inside the sonicated areas as well as in nearby organs is of fundamental importance in order to avoid excessive overheating in unwanted areas, that may lead to skin burns.
Considering this, the still open issues in MRgFUS treatment can be traced to (I) the assisted segmentation of the ROI target; (II) the improvement of techniques for temperature monitoring within the ROI; and (III) the compensation of patient motion during treatment.
Assisted segmentation of target regions
Before MRgFUS treatment, it is necessary to obtain a detailed morphological map of the anatomical district of interest, where the ROI to be ablated and any areas/organs not affected by the ultrasound beam (bowel loops, bones and other organs) will be selected. Moreover, after MRgFUS treatment, in order to get a first qualitative and quantitative evaluation, the volume of ablated fibroid is manually marked by the operator who selects (on each slice from a MR dataset acquired at the end of treatment with contrast agent) the ROI that has been effectively treated.
All these operations are based on completely manual approaches, which are operator-dependent and time-consuming. This working methodology does not warrant a valid metric for the objective planning and evaluation of treatment outcome, in ROI selection (pre-treatment phase) as well as in the detection of ablated fibroids area (post-treatment phase). Considering this scenario, it would be useful to improve this selection process by implementing tools for automatic/semi-automatic segmentation of regions, which can assist the operator in the planning and evaluation phases of MRgFUS treatment.
In the literature there are few works related to fibroids segmentation issues, presenting mainly semi-automated approaches. In study (12) an automated fibroids segmentation approach for fibroids volume evaluation from MR images is presented. Firstly, a fuzzy C-means (FCM) algorithm is used to segment the uterus from a T1w-enhanced dataset. Successively some morphological operations are applied to refine the initial segmentation results. Redundant parts are removed by masking registered the T1w dataset with a mask obtained from a previous T1w-enhanced dataset segmentation and using histogram thresholding. Afterwards, fibroids are segmented by applying a modified possibilistic fuzzy C-means (MPFCM) algorithm on registered T2w images and some post-processing operations. In another study (13) the authors propose a semi-automatic method based on the level-set, where the active contours of the ROI evolve following the trend of a signed function, just for the segmentation of uterine fibroids and the subsequent volume measurement. The overall method combines a fast marching level set and a Laplacian level set. The region growing approach is well suited to the segmentation of a single area, but some patients show a pathological scenario with multiple uterine fibroids. In another study (14) a semi-automatic approach based on multi-seed region growing segmentation is proposed, allowing the selection and segmentation of two or more unconnected treated areas (Figure 2).
Typical segmentation methods, found in the literature, can be divided into one of the following classes: thresholding, edge-detection, clustering, active contour, soft computing (e.g., fuzzy or neural networks approaches) and direct region detection. Thresholding segmentation techniques have the advantage of greater computational simplicity, but do not always give good results. This leads to the need of further post-processing steps. Techniques based on edge-detection allow the extraction of the contours associated with high gradient areas. Unfortunately sometimes the edges are not well defined, obtaining incorrectly segmented ROIs. Clustering approaches need to know the number of clusters, and such information is not always available a priori. Active contour segmentation techniques are widely used in medical imaging, but involve the setting of many parameters and this can represent an issue for physicians with not many computer skills. Direct region detection approaches can obtain well-defined ROIs with closed contours, showing good processing-time and rapid applicability because of the few parameters to be set.
Direct region detection theory
Direct region detection tries to find regions on the basis of global considerations (15). This can be seen in terms of functional approximation, where the image I = f (x, y) is considered as a brightness function defined on a spatial domain R, which has to be divided into the minimum number of regions that satisfy uniformity conditions (16). These constraints are expressed by a logical predicate P {Eq. [1]} defined on a generic subset S of R ():
The selection of similarity criteria depends on the examined problem as well as on the features of available image data.
A segmentation of the picture I is represented by the partition of its own domain R (the entire image region) into regions (subsets of R) {Ri},i=1,...,n, for some n (not unique) such that {Eq. [2]}:
where Ri and Rj are spatially adjacent sub-regions in R (i.e., forms a connected set).
Region detection methods can be therefore divided into two types:
- Bottom-up (merging): the picture is divided into partitions, also coinciding with single pixels, which are then merged to form larger regions. In fact, a merging scheme starts with a partition of R satisfying [2.d] and achieves condition [2.e];
- Top-down (splitting): the entire image is recursively split into partitions until certain criteria are matched. Dually with respect to merging, a splitting procedure begins with a partition of R that meets [2.e] and proceeds to fulfil [2.d].
In the next section, the region growing method is described with more details.
Region growing segmentation algorithm
Region growing is one of the most widely used bottom-up segmentation methods. It aims to produce a homogeneous region by successively merging primitive regions (even single pixels) (15). Therefore, the region growing approach starts from a seed (one or more pixels inside the ROI) and proceeds to search a local connected region on the basis of a given similarity measure and a pixel connectivity property. The output is thus a set of mutually exclusive regions. This technique ensures simplicity and good performance in medical image segmentation.
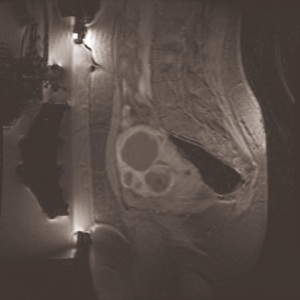
As depicted in Figure 3, after MRgFUS treatment, fibroids appear as homogenous hypo-intense regions with respect to the uterus, thus making region growing an appropriate segmentation approach because it is founded on local similarity assumption. Thereby, connected pixels are assigned to the same class if a region membership criterion (specified by a logical predicate P) is satisfied.
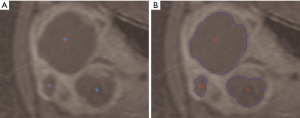
Since the number of fibroids is not a priori known in pathological scenarios of patients affected by several fibroids, a multi-seed region growing segmentation is required. Accordingly, each region independently begins its own growth from an identifying pixel. The initial seed-points set must be then an expressive sample of the ROI. Seed selection, accomplished by an expert radiologist during treatment, affects overall segmentation results and represents a very critical task (17). Moreover, the region growing procedure must be interrupted if no more pixels match the membership criterion, expressed by a stopping rule (15). The inclusion in a region can be formalized in terms of a segmentation threshold, which guides the homogeneity decision test by specifying the maximum allowed intensity variation of the pixels within the ROI (18).
In conclusion, starting from the selected seed-points, the region growing algorithm analyzes the neighbours of the current pixel. For each of these neighbours, the condition Eq. [3] must be matched. This relation defines the Boolean predicate P and is composed by three sub-conditions, expressed respectively by Eqs. [4-6], checking if:
- The pixel is inside the image;
- The pixel has not already been added in the ROI;
- The pixel value satisfies the condition on the threshold ThRG.
In our implementation, the predicate RGcondition can be defined on the generic pixel (i, j) belonging to the input image I = f (x, y) of size M × N:
with:
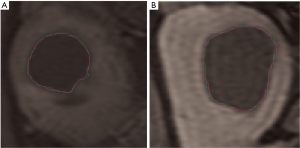
Assuming the segmentation performed manually by an expert radiologist as our gold standard, the goodness of the results can be objectively evaluated by quantifying the difference between manual and automatic segmentation. Two sample images are shown in Figure 4.
Enhancement of temperature monitoring during treatment
Techniques for temperature measurement during MR-guided treatment are mainly based on the PRF thermometry or its variants (19). PRF shift provides a method to measure temperature changes during MRgFUS thermotherapy. The temperature sensitivity of PRF, which exploits water proton chemical shift induced by the temperature changes, was observed firstly by Hindman (20). MRI-derived temperature maps can be constructed using a gradient-recalled echo (GRE) imaging sequence by measuring the phase variation resulting from the temperature-dependent change in resonance frequency (21).
Proton resonance frequency theory
Phase variations are proportional (I) to the temperature-dependent PRF change; and (II) to the echo time TE, and they can be converted to a temperature change according to the following Eq. [7]:
where:
- φ(T) is the phase in the current image;
- φ(T0) is the phase of a reference (baseline) image at a known temperature;
- γ is the gyromagnetic ratio;
- α =–0.01 ppm/°C is the PRF change coefficient;
- B0 is the magnetic field strength;
- TE is the echo time.
Conventional PRF thermometry works by subtracting the phase-map baseline image from the current map. The PRF-based approaches have some limitations, such as the dependence on the reference thermal image (baseline). Any misalignment with respect to the baseline (due by tissue/patient movement or by resonance frequency drift) causes the generation of artefacts in the maps and errors in temperature measurement.
Motion artefacts can be divided into two categories: intra-scan motion and inter-scan motion. Intra-scan motion is caused by movement of an object during MR image acquisition, resulting in a poor quality image with typical blurring and ghosting artefacts. These motion artefacts are not specific to PRF temperature imaging and can be reduced by accelerating the image acquisition. Inter-scan motion is due to movement or displacement of an object between the acquisitions of consecutive images (22). Where movement occurs, the methods used for temperature estimation can be divided into two categories: (I) multi-baseline methods; and (II) referenceless methods.
Referenceless methods for temperature estimation
Multi-baseline methods collect background phase information at various stages of the respiratory and/or cardiac cycle prior to heating, so that baseline data exist for all positions of the organ. The baseline subtraction is then performed by matching the image acquired during heating with the corresponding stored baseline data in order to mitigate motion-induced misregistration. The selection of the corresponding baseline image is performed by determining the organ’s position with a navigator echo or based on a similarity criterion, such as non-similarity coefficients or inter-correlation coefficients (19,23,24). The multi-baseline methods require cyclic organ motion in order to acquire a full set of all possible baseline images and require additional setup time to assemble the baseline library. They are generally much more robust to motion than conventional baseline subtraction, but remain sensitive to susceptibility changes during therapy.
Referenceless methods estimate heating from a treatment image itself, without a baseline image used as temperature reference. Operating under the assumption that the phase image (surrounding the treated region) has a soft and smoothed trend even under the heated area, referenceless thermometry methods fit a set of smooth, low-order polynomial functions to the surrounding phase or to a complex magnitude image with the same phase using a weighted least-squares fit (25,26). The extrapolation of the polynomial inside the heated region serves as background phase estimation, which is then subtracted from the actual phase to evaluate the phase difference before and after heating caused by ultrasound sonication.
Considering this, in classical PRF shift thermometry there are obvious problems of artefacts, most prevalently due to motion, and in referenceless thermometry the accuracy of the interpolation lacks precision, radial basis function (RBF) approach (Figure 5) can be applied to these thermometry issues (27).
Radial basis function interpolation
Consider a real function of d variables that must be approximated by , given the values , where is a set of n distinct points in , called the interpolation nodes. This approximation can be represented as {Eq. [8]}:
where:
- Pm is a low-degree polynomial;
-
denotes the Euclidean norm;
- φ is a fixed function from
to
.
Thus, the radial basis function s is a linear combination of translations of the single radially symmetric function , plus a low-degree polynomial. We will denote with the space of all polynomials of degree m at least in d variables. Then λi coefficients of the approximation s are determined by requiring that s satisfies the interpolation conditions expressed by the following Eq. [9], together with the side conditions in Eq. [10]:
Some examples of popular choices of φ and the corresponding radial function are given below:
where a and c {Eq. [11]} are positive constants. Some typical conditions on the nodes under which the interpolation conditions Eqs. [9,10 uniquely specify the radial basis function Eq. [8] are given in Table 1. In this context, “not coplanar” means that the nodes do not all lie in a single hyper-plane, or equivalently that no linear polynomial in d-variables vanishes at all of the nodes. The surveys of Powell and Light are excellent references for these and other properties of radial basis functions (28,29).

Full table
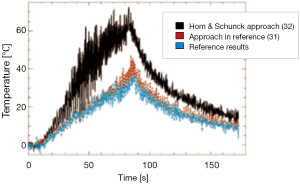
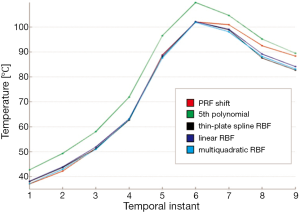
Figure 6 shows a comparison among temperatures calculated with standard PRF shift, polynomial method, linear RBF, thin-plate spline RBF, and multiquadratic RBF for a chosen point along the successive temporal instants of the treatment. Polynomial reconstruction over-estimates the temperature: this can lead to stop the sonication before reaching the temperature established with the risk of not producing the desired protein denaturation.
It is intuitive to understand how, to address properly the problem of temperature measurement, it is necessary to integrate this problem with motion compensation.
Patient motion-compensation
For the success of MRgFUS treatment, it is fundamental that the patient undergoing thermal ablation remains stationary. Patient movements may be caused by voluntary (for example, a reaction to pain during treatment) or involuntary movements (of internal organs, related to respiration, heartbeat, intestinal peristalsis). As a consequence, such movements can lead to (I) a displacement between the planned ROI and the real position of the various anatomical ROIs; and (II) artefacts in the thermal maps used to monitor the temperature of the ROI treated with ultrasound, due to mismatches between the baseline and the current thermal map.
Therefore, there is the need for algorithms that track targets when body motion is involved and compensate these movements, making it possible to (I) reposition the ROI without the need to re-plan the entire treatment; and (II) improve the temperature measurement, eliminating/reducing the misalignment between thermal maps.
Motion correction approaches
In literature there are several approaches to correct patient motion (30-33). One approach, used to compensate organ displacement and deformation, uses image registration based on the magnitude images which represent the anatomical information (34). Optical flow algorithms estimate complex motion and were recently demonstrated to be a good solution for motion stabilized MR-thermometry on abdominal organs (35). Other approaches refer to the modelling of the phase changes induced by motion and artefact estimation by extrapolation from areas not affected by temperatures changes (25,36). The approach proposed in reference (37), based on phase correction tables, is justified by the consideration that motion is caused by the respiratory or the cardiac cycle. Considering the intrinsic periodicity of these movements, a phase lookup table (prior to MR-thermometry) which covers the entire motion cycle can be established, to make it possible (during MR-thermometry) for a given organ position to give the corresponding phase correction. Since the difference represents only temperature-related phase changes, the correct temperature can be estimated (30).
Optical flow motion correction
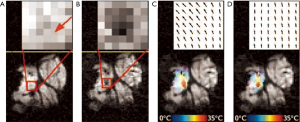
Optical flow is defined as the change of structured light in the image, due to a relative motion. As discussed in reference (38), optical flow algorithms estimate a velocity field by assuming an intensity conservation during displacement between temporally-consecutive images (Figure 7).
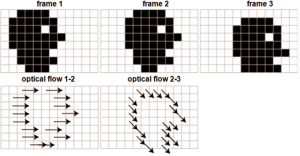
According to the following Eq. [12], this algorithm can be mathematically expressed by the optical flow constraint equation (OFCE):
where:
- u and v are the 2D displacement vector components;
- Ix,Iy,It are the spatio-temporal partial derivatives of the image pixel intensity.
Since a direct estimation by minimizing the deviation from OFCE is an under-determined problem, additional constraints, over that shown in Eq. [12], are required. Horn and Schunck in reference (39) proposed to use the physical constraints such as elasticity, which can be expressed as the smoothness of the motion field in the neighbourhood of the estimation point, according to the following Eq. [13].
where:
- a is a weighting factor, designed to link the two individual metrics (intensity variation and motion regularity) and which has to be optimized for any given motion pattern.
In particular, a high value of a2 increases the robustness against noise and local intensity variations which would otherwise be incorrectly attributed to motion. Moreover, high a2 values prevent the correct estimation of large motion amplitudes and complex motion patterns which display large motion gradients, such as shearing.
For the particular case of motion estimation based on magnitude images during hyperthermia treatments, temperature variations and tissue modifications lead to a variation of the local T1 and T2 relaxation times and thus to local intensity modifications. Consequently, the condition of energy conservation of the OFCE is locally violated and might thus lead to incorrect motion estimates.
In the work described in reference (38), the physical cause of the intensity perturbation (the local temperature change) is integrated into the motion estimation algorithm (Figure 8). This is achieved by using the temperature map of the most recently acquired dataset to adapt the local weights of confidence in the intensity conservation of the subsequently acquired new image. As illustrated in Figure 9, this last approach makes it possible to enhance temperature estimation.
Conclusions
MRgFUS is an innovative technology which offers a number of advantages in the treatment of symptomatic uterine fibroids over traditional surgical resection, such as (I) maintenance of the reproductive capacity, thanks to the non-invasive nature of this treatment; and (II) reduction of hospitalization time.
However, there are some issues that need to be addressed to further improve the whole therapeutic process, such as (I) the assisted segmentation of the ROI target in the pre-treatment planning phase as well as in the post-treatment NPV evaluation phase; (II) the improvement of MR-based techniques for temperature monitoring in the treatment of ROIs as well as in the areas of patient-machine interface, to prevent burns on the patient skin; and (III) the compensation of patient motion during treatment.
Considering the wide variety of approaches and solutions found in the literature about these three issues, this work was limited to a high-level argumentation, providing a general scenario that provides a clear and concise comprehension of the problems and how each of them affects the MRgFUS treatment. Subsequently, technical details about a specific approach were provided that are considered a useful starting point for further study and research.
Acknowledgments
Funding: This work was supported by “Development of a New Technological Platform Based on Focused Ultrasounds for Non Invasive Treatment of Tumours and Infections” project (PON01_01059) and by “Smart Health 2.0” MIUR project (PON04a2_C).
Footnote
Provenance and Peer Review: This article was commissioned by the Guest Editors (Giusi Irma Forte and Giorgio Russo) for the series “High intensity focused ultrasounds” published in Translational Cancer Research. The article has undergone external peer review.
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.3978/j.issn.2218-676X.2014.09.06). The series “High intensity focused ultrasounds” was commissioned by the editorial office without any funding or sponsorship. The authors have no other conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Ryan GL, Syrop CH, Van Voorhis BJ. Role, epidemiology, and natural history of benign uterine mass lesions. Clin Obstet Gynecol 2005;48:312-24. [PubMed]
- Verkauf BS. Changing trends in treatment of leiomyomata uteri. Curr Opin Obstet Gynecol 1993;5:301-10. [PubMed]
- Machtinger R, Inbar Y, Cohen-Eylon S, et al. MR-guided focus ultrasound (MRgFUS) for symptomatic uterine fibroids: predictors of treatment success. Hum Reprod 2012;27:3425-31. [PubMed]
- Chapman A, ter Haar G. Thermal ablation of uterine fibroids using MR-guided focused ultrasound-a truly non-invasive treatment modality. Eur Radiol 2007;17:2505-11. [PubMed]
- Roberts A. Magnetic resonance-guided focused ultrasound for uterine fibroids. Semin Intervent Radiol 2008;25:394-405. [PubMed]
- Hurwitz M, Machtinger R, Fennessy F. Magnetic resonance-guided focused ultrasound surgery for treatment of painful osseous metastases. Progress in Biomedical Optics and Imaging, ISSN1605-7422, 2011, vol. 12, no19, [Note(s): 79010M.1-79010M.9].
- McDannold N, Clement G, Black P, et al. Transcranial MRI-guided focused ultrasound surgery of brain tumors: Initial findings in patients. Neurosurgery 2010;66:323-32. [PubMed]
- Kopelman D, Inbar Y, Hanannel A, et al. Magnetic resonance-guided focused ultrasound surgery (MRgFUS): ablation of liver tissue in a porcine model. Eur J Radiol 2006;59:157-62. [PubMed]
- Stewart EA, Gostout B, Rabinovici J, et al. Sustained relief of leiomyoma symptoms by using focused ultrasound surgery. Obstet Gynecol 2007;110:279-87. [PubMed]
- Hesley GK, Felmlee JP, Gebhart JB, et al. Noninvasive treatment of uterine fibroids: early Mayo Clinic experience with magnetic resonance imaging-guided focused ultrasound. Mayo Clin Proc 2006;81:936-42. [PubMed]
- Bohlmann MK, Hoellen F, Hunold P, et al. High-Intensity Focused Ultrasound Ablation of Uterine Fibroids - Potential Impact on Fertility and Pregnancy Outcome. Geburtshilfe Frauenheilkd 2014;74:139-45. [PubMed]
- Fallahi A, Pooyan M, Khotanlou H, et al. Uterine fibroid segmentation on multiplan MRI using FCM, MPFCM and morphological operations. Computer Engineering and Technology (ICCET), 2nd International Conference. 16-18 April 2010;7:1-5.
- Yao J, Chen D, Lu W, et al. Uterine fibroid segmentation and volume measurement on MRI. Proc. SPIE 6143 Medical Imaging 2006;6143:640-9.
- Militello C, Vitabile S, Russo G, et al. A semi-automatic multi-seed region-growing approach for uterine fibroids segmentation in MRgFUS treatment. CISIS Conference 2013:176-88.
- Gonzalez RC, Woods RE. eds. Digital Image Processing. 3rd ed. Prentice Hall, 2007.
- Horowitz SL, Pavlidis T. Picture Segmentation by a Tree Transversal Algorithm. J Assoc Comput 1976;23:368-88.
- Adams R, Bischof L. Seeded region growing, pattern analysis and machine intelligence. IEEE Trans Image Process 1994;16:641-7.
- Chang YL, Li X. Adaptive image region-growing. IEEE Trans Image Process 1994;3:868-72. [PubMed]
- Rieke V, Butts K MR. Thermometry. J Magn Reson Imaging 2008;27:376-90. [PubMed]
- Hindman JC. Proton resonance shift of water in gas and liquid states. J Chem Phys 1966;44:4582-92.
- Ishihara Y, Calderon A, Watanabe H, et al. A precise and fast temperature mapping using water proton chemical shift. Magn Reson Med 1995;34:814-23. [PubMed]
- Vigen KK, Daniel BL, Pauly JM, et al. Triggered, navigated, multi-baseline method for proton resonance frequency temperature mapping with respiratory motion. Magn Reson Med 2003;50:1003-10. [PubMed]
- Shmatukha AV, Bakker CJ. Correction of proton resonance frequency shift temperature maps for magnetic field disturbances caused by breathing. Phys Med Biol 2006;51:4689-705. [PubMed]
- Roujol S, Ries M, Quesson B, et al. Real-time MR-thermometry and dosimetry for interventional guidance on abdominal organs. Magn Reson Med 2010;63:1080-7. [PubMed]
- Rieke V, Vigen KK, Sommer G, et al. Referenceless PRF shift thermometry. Magn Reson Med 2004;51:1223-31. [PubMed]
- Kuroda K, Kokuryo D, Kumamoto E, et al. Optimization of self-reference thermometry using complex field estimation. Magn Reson Med 2006;56:835-43. [PubMed]
- Agnello L. Referenceless Thermometry using Radial Basis Function Interpolation. International Conference on Computer Medical Applications 2014.
- Powell MJ. The theory of radial basis function approximation in 1990. In: Light WA. eds. Advances in Numerical Analysis II: Wavelets, Subdivision Algorithms and Radial Functions. Oxford, UK: Oxford University Press, 1992:105-210.
- Light WA. Some aspects of radial basis function approximation. In: Singh SP. eds. Approximation Theory, Spline Functions and Applications. Dordrecht: Kluwer, 1992:163-90.
- Maclair G, de Senneville BD, Ries M, et al. PCA-Based Image Registration: Application to On-Line MR Temperature Monitoring of Moving Tissues. ICIP 2007;3:141-4.
- Ross JC, Tranquebar R, Shanbhag D. Real-time liver motion compensation for MRgFUS. Med Image Comput Comput Assist Interv 2008;11:806-13. [PubMed]
- Schwartz B, McDannold N. MRI Motion Compensation by Positional Ultrasound Biometrics. Proc Intl Soc Mag Reson Med 2011;19:3721.
- Ries M, Denis de Senneville B, Maclair G, et al. Three dimensional motion compensation for real-time MRI guided focused ultrasound treatment of abdominal organs. AIP Conference Proceedings 2010;1215:243-6.
- Maintz JB, Viergever MA. A survey of medical image registration. Med Image Anal 1998;2:1-36. [PubMed]
- Roujol S, Ries M, Quesson B, et al. Real-time MR-thermometry and dosimetry for interventional guidance on abdominal organs. Magn Reson Med 2010;63:1080-7. [PubMed]
- Salomir R, Denis de Senneville B, Moonen CTW. A fast calculation method for magnetic field inhomogeneity due to an arbitrary distribution of bulk susceptibility. Concept Magn Reson B 2003;2003:19B.
- Denis de Senneville B, Quesson B, Desbarats P, et al. Image Processing, 2004. ICIP 2004;4:2571-4.
- Roujol S, Ries M, Moonen CT, et al. Robust real time motion estimation for MR-thermometry. ISBI 2011:508-11.
- Horn B, Schunck B. Determining optical flow. Artificial Intelligence 1981;17:185-204.