Dosimetry implications for correct ultrasound dose deposition: uncertainties in descriptors, planning and treatment delivery

Introduction

Ultrasound (US) is used as an energy source for ablative treatments of tumours of the liver, prostate, kidneys, lung, brain, bone and uterine fibroids (1,2). Interest in its use for treatments that combine hyperthermia and radiotherapy is returning, as is the use of “non-thermal” US exposures for the enhancement of drug delivery. With this growing acceptance of US as an important therapeutic tool, the need for accurate, standardised, and repeatable measures of dose becomes increasingly important. These are particularly required for treatment planning, where the dose defines the objective functions used to optimise the transducer parameters (specifying delivery of the required treatment, such as the phase and amplitudes applied to individual elements of a phased array).

Although therapy US is currently planned and monitored in real time using US or magnetic resonance (MR) imaging, pre-treatment simulation for planning purposes can have significant advantages. Choice of the optimum treatment window and beam path can be difficult without simulation, especially when bone, gas or other sensitive normal structures lie between the skin and the target to be exposed. Simulation allows it to be possible to be sure that the exposure level to critical tissues is safe. Current clinical practice for HIFU involves locating the target using US or MR imaging, and outlining the region to be treated. Accurate target identification is based on the imaging response following a “test” or “siting” US exposure (3). Under US guidance, tissue response is gauged by the appearance of new bright echoes in the grey scale image (4), although passive acoustic mapping techniques can also be used to determine whether inertial cavitation has occurred during exposure (5). The grey scale response is produced by scattering from “boiling” bubbles produced in the focal region (6). Once these are seen, irreversible tissue damage has occurred. With MR guidance, the aim of these test shots is to detect the magnitude and position of the temperature rise induced, using thermometry sequences (7). The accuracy of this method depends on the spatial and temporal resolution of the sequences used. While these techniques work in principle, considerable time is expended in finding the correct exposure conditions, and optimum acoustic window for any given treatment. Planning prior to treatment delivery, may significantly shorten HIFU sessions.

In US therapy, there is considerable confusion between the concepts of “exposure” and “dose”, with the terms frequently being used interchangeably. The term “exposure” in the context of radiation refers to the amount of energy incident on the target of interest. In photography, before the digital age, the exposure was described in terms of both the light intensity, and the time for which the film was exposed. Similarly, for US, the exposure should be described in terms of the acoustic field, preferably that incident on the target, and the insonation time. The US field may be given in terms of acoustic pressure, or of intensity. Dose parameters have been defined for ionising radiation. Absorbed dose (mGy) is defined as the amount of incident energy absorbed, equivalent dose (mSv) describes the biological impact of the radiation on tissue, and effective dose (mSv) takes into account both radiation type and the tissue sensitivity. No such dose parameters exist for US.

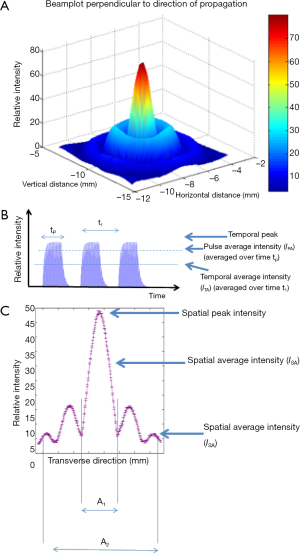
A well validated dose parameter is an important goal for therapy US. It would allow prediction of the biological effect, inter-comparison of treatments (and, perhaps more importantly, of side effects) on the same machine, and on different devices. In the absence of such a parameter, clinical and pre-clinical treatments are variously and inconsistently reported. The literature shows that the descriptive parameters used include spatial peak, temporal averaged intensity (I_SPTA), temporal averaged intensity (I_TA), spatial average, temporal averaged intensity, and a number of peak pressure parameters (see Figure 1). These are all measures of the exposing field, not the dose, and provide no useful information for treatment assessment and comparison unless the time of exposure, beam geometry, and tissue parameters are also known.

Figure 1 (A) Typical beam distribution in the focal plane for a focused ultrasound beam; (B) example of a pulse train for therapy ultrasound, showing the temporal variation; (C) typical transaxial profile at the focus for a therapy ultrasound beam, showing the different possibilities for temporal and spatial averaging.

Where the primary mechanism for US induced biological effect is thermal, it may suffice to describe the US treatment in terms of a “thermal dose”, especially for “non-ablative exposures”. Validation of this concept for the short duration, high temperature treatments required for ablation has proved to be technically difficult. Sapareto & Dewey (8) introduced a method by which thermal treatments, undertaken at different temperatures and heating times, can be compared. On the basis of experimental data, they divided thermal response into two regions, above and below 43 °C. Although they describe the choice of breakpoint of 43 °C as being “arbitrarily chosen as the best estimate”, this has become the de facto baseline temperature to which all thermal treatments are now compared. Thermal dose is thus usually described in terms of cumulative equivalent minutes at 43 °C, CEM₄₃ (see section on Thermal dose calculations). While this term is commonly used to plan ablative therapies with a CEM₄₃ of 240 minutes being used as the threshold for success, it has not yet been satisfactorily validated for temperatures above 55 °C.

Ultrasonic interaction with tissue also leads to non-thermal effects. At therapy exposure levels, the most important of these is cavitation (6). Defining a dose for cavitation mediated events is more problematic than for those caused by heating. To date, only an inertial cavitation dose (ICD) has been addressed (9). The ICD is most usually obtained by integrating broadband emissions, characteristic of this collapsing bubble activity, over the time period of interest. While this gives a relative measure of the amount of cavitation activity, the value obtained depends on the detection systems and exposure geometry being used [see section on Inertial cavitation dose (ICD)].

No method of combining these thermal and non-thermal dose concepts has been proposed. In reality, for many exposure regimes, the two classes of interaction mechanism occur together, with, for example, an increase in temperature increasing the probability of the occurrence of inertial cavitation.

The structure of this paper is based on the protocol for successful delivery of a focused US treatment at an intended dose. A review of the range of existing dose descriptors is presented, and then the requirements for treatment planning and the uncertainties associated with acquiring the pre-clinical images and the errors which may affect treatment delivery are discussed. Broadly there are three uncertainties arising from preclinical images: (I) errors in segmentation of the images and in determining relevant associated acoustic and thermal properties; in order to compute the dose (II) registration errors arising from differences in pre and intra-operative images (III) artefacts associated with organ motion and deformation. From the definition of dose and the requisite preclinical data, the final section outlines the errors associated with treatment planning and delivery, based on focusing techniques and on lesioning strategies which use either single or multiple foci.

Existing descriptors

In this section we review existing descriptors for both exposure and dose, and their origins.

Exposure

Acoustic field models

The governing equations for ultrasonic wave propagation in a fluid can be derived from the equations of motion, continuity and heat transfer, and an equation of state (10,11). The most complete, yet computationally tractable, model of the acoustic field is the Westervelt equation (12) (Eq. [1]):

∇2p−1c02∂2p2∂t2+δc04∂3p∂t3+βρc04∂2p2∂t2=0[1]

where p is the pressure, and c₀ is the speed of sound, or, for axi-symmetric, weakly focused fields, the parabolic Khokhlova-Zabolotskaya-Kuznetsov (KZK) equation (11) (Eq. [2]):

∂2p∂z∂τ=c02∇⊥2p−δ2c03∂3p∂τ3−β2ρc03∂2p2∂τ2,∇⊥2p=∂2p∂x2+∂2p∂y2[2]

where τ = t – z/c₀ is the retarded time variable and z is the direction of propagation. The nonlinearity parameter is denoted by β and the sound diffusivity, δ, is a function of the bulk and shear viscosities, thermal conductivity and specific heat capacities at constant volume and pressure. As the acoustic field propagates through tissue the energy is reduced (attenuated). The attenuation is due to both scattering and absorption effects, and is characterised by the attenuation coefficient, α, which can be expressed as (Eq. [3]):

α=αabs+αscat[3]

where α_abs and α_scat are the absorption and scattering coefficients respectively.

Acoustic holography, or an equivalent source method, can provide suitable initial conditions for the Westervelt and KZK equations (13,14).

Thermal models

It can be shown that, on the scales considered for ultrasonic wave propagation, thermal effects are negligible, in that the acoustic field and the temperature field decouple and the temperature field can be computed from the acoustic field (10). The three primary heat sources resulting from US exposure are: absorption, shock-wave and cavitation heating.

Absorption

The absorption of an US wave in water is primarily due to viscosity (described by Stokes’ Law), and results in an attenuation coefficient proportional to the square of the frequency, relating δ to the total attenuation α. In tissue absorption is dominated by a wide range of relaxation mechanisms. Within therapeutically relevant parameters, the absorption of US by tissue is well characterised by a frequency dependent power-law (15) (Eq. [4]):

αabs=α0wy,1<y<2[4]

The computational implications of this power-law are that for situations in which it cannot be assumed that exposure is continuous, such as for short pulsed exposures, modelling requires fractional-differential operators (16), or the computation of a large number of relaxation processes (17,18).

The conversion of pressure into a heat source is achieved by taking the dot product of the linearized momentum equation, which can be expressed in conservation law form as (Eq. [5]):

∂E∂t+∇⋅I=0[5]

For a plane progressive wave in a homogeneous medium without scatter (Eq. [6]):

E=12p2ρc02I=np2ρc02[6]

where E is the energy per unit volume and n is the unit normal in direction of propagation. This equation expresses the instantaneous rate of energy deposition per unit volume and defines the dissipation function,, where I is the instantaneous acoustic intensity given by I = pv. This quantity has utility, but is unwieldy. A range of descriptors which may be spatially or temporally varying, or may be scalar quantities can be derived. Indeed, many authors, e.g(19), refer to the intensity as the time-averaged intensity, I = I_TA = <pv>. This may be normalised over the duration of the exposure to give the pulse-averaged intensity, I_PA. The temporal peak intensity, I_TP, may be a better descriptor for focused fields. However, since quantities are spatially varying, the scalar values provided by spatial peak, temporal averaging, I_SPTA, or the spatial-average, temporal average, I_SPTA, can be used to characterise the field. These concepts are illustrated in Figure 1. Nyborg showed that for a plane progressive wave in a homogeneous medium, the dissipation per unit volume can be given by q_v=2αI_TA.

The dissipation factor has also been referred to as the specific absorption rate (SAR). This is widely used as the standard measure of dose in hyperthermia treatment planning with electromagnetic sources. However, in acoustics, the dissipation of the acoustic energy and the absorption of the acoustic energy by tissue are not equal, as scattering also contributes.

Duck (20) defines the dissipation function per unit mass, as the acoustic dose rate, which is integrated with respect to time to give the acoustic dose, Φ. This definition naturally extends to fields with a distribution of frequencies.

Nonlinear propagation

When the amplitude of the particle velocity is large, nonlinear processes transfer acoustic energy from the fundamental frequency to higher harmonic components. These are important as they have shorter wavelengths than the fundamental, and the focal volume is therefore smaller. Furthermore, as shown by equation (4), these higher frequencies are preferentially absorbed. Soneson and Myers (21) showed that the difference in thermal dose computed from linear and nonlinear wave equations for low duty cycles may not be significant after a cooling-off period, due to heat diffusion from within a tightly focused nonlinear field.

As nonlinear processes lead to an accumulation of higher harmonic components, the wave steepening can lead to shock-type waves) (22). The presence of a discontinuity leads to significantly different physics. Neglecting dissipative terms, and considering an integral form of the energy conservation equation (11) around the shock front yields (Eq. [7]):

dEdt=−β6ρ02c03(ΔP)3[7]

This shows that, in the presence of shocks, the energy may be absorbed by the medium even in the explicit absence of dissipation mechanisms. Care is needed in interpreting this result as, since tissue is attenuating, true shocks will never exist, but shock-like waves with very steep wave fronts can occur. However, these shock-like waves can be considered approximations to true shocks, and for effectively attenuation can be considered to be the sum of the shock and classical absorption mechanisms. The absorption at the shock interface is proportional to the cube of the shock amplitude, whereas for classical absorption it is proportional to the square of the pressure amplitude (Eq. [6]). Thus, although absorption provides a non-negligible contribution to heating, within the parameter regimes in which shock-type waves appear, the dominant mechanism of heat generation will be shockwave heating (23,24).

Cavitation

The third mechanism for heating is cavitation. The presence of nucleation sites and dissolved gas may, for some regimes, result in cavitation activity during US exposure (1,6). Cavitation activity may either enhance or inhibit heat deposition within the target region. If cavitation occurs within the focal volume, heating may be enhanced. As described below, this results from viscous effects at the inertially cavitating bubble surface and also from absorption of the broadband emissions characteristic of this activity (25). Where cavitation occurs pre-focally, scattering from the bubbles formed may effectively shield the focal region from receiving sufficient energy to ablate the tissue in the target volume, and may lead to pre-focal tissue damage (26).

Thus, the thresholds at which cavitation activity can be reliably detected have attracted a great deal of attention. This activity has typically been quantified using passive detection of the broadband emissions and their integration.

There are a number of governing equations which can be used to model the dynamics of an oscillating bubble in an ultrasonic field, including those of Herring, Gilmore or Rayleigh-Plesset (27-30). From the Rayleigh-Plesset equation, Flynn (31) defined four descriptors for cavitation: stable and transient, which characterise the life cycle of the bubble, and inertial and non-inertial, which characterise the nature of the collapse of the bubble. Based on a stably oscillating bubble undergoing repeated inertial collapse, Hilgenfeldt et al. (32), Holt and Roy (25) postulated three mechanisms for heat deposition from bubble dynamics:

• Absorption of shockwaves emitted during inertial collapse of the bubble;
• Viscous heating arising from the motion of the bubble wall;
• Conduction between the internal gases and vapour, heated during the inertial collapse, and the surrounding medium.

By considering therapeutically relevant parameters Hilgenfeldt et al. were able to compare the thermal contributions from each of these three effects. They found that the primary mechanism for heat deposition from micron sized bubbles in the 1-2 MHz range, driven at intensities which produced peak and negative pressures of 2 MPa, was typically the absorption of shockwaves from the inertial collapse of a bubble. The contributions from viscous heating could be important, and the contribution from thermal conduction was found to be significantly lower.

The thermal field is computed using the Pennes Bioheat Transfer Equation (33). This accounts for bulk blood perfusion as (Eq. [8]):

cvρ∂T∂t=∇⋅(k∇T)+qi+v(T−T∞)[8]

where c_v is the specific heat capacity, ρ is the density, κ is the thermal conductivity, q_i are heat sources due to absorption, shockwave heating and cavitation, v is the bulk perfusion parameter and T_∞ is the ambient temperature. The effect of perfusion appears as an isotropic, homogeneous cooling term which reaches instantaneous thermal equilibrium.

One deficiency of this model, noted by Pennes, is its assumption that heat transfer between blood and tissue occurs only in the capillaries. Later studies have shown that there is a critical size which demarcates vessels which primarily cool tissue and from which heat surround tissue (34-38). For single vessels this effect can be modelled as a bulk property, but for concurrent networks of vessels, the average flow is almost zero and the effect of perfusion acts to increase the effective conductivity of the tissue. An alternative approach is to consider the evolution of three temperatures fields—tissue, venous and arterial. This approach was explored by Keller & Seiler (37) and several modifications have since been proposed (39-41). These are expected to be more accurate, but rely on deriving effective medium properties for thermally significant vessels which may not be visible. Asymptotic homogenisation uses a form of averaging to couple a discrete regular vascular structure with tissue into a single effect medium model to overcome the problem of modelling vascular structures on a scale which is smaller than the resolution provided by medical imaging (42). Discrete modelling is possible for thermally significant blood vessels which can be imaged (43). This is important since vessels greater than 1 mm in diameter can significantly affect the thermal dose delivered during ablative therapies, due to advected heat transfer. This can lead to unwanted tissue-sparing (thus increasing the risk of disease recurrence), asymmetric dose (44) and/or the over-treatment of healthy tissue. Furthermore, regions with large, thermally significant vessels require a greater US exposure, involving either higher intensity, or longer treatment times (45).

Knowledge of the thermal field is important for the calculation of the thermal dose, as the acoustic and thermal parameters have a well characterised temperature dependence (46). Pseudo-spectral spatial domain methods are typically employed in the computation of nonlinear acoustic fields, [e.g., (47)]. That is, in a given plane, the acoustic field is calculated for all times and as such struggle to include phenomena which evolve in time such as cavitation, or changes in material properties with temperature.. These may be significant as they can lead to thermal lensing, in which changes in the material properties result in a shift in the focus. With the exception of fat, an increase in temperature will raise the speed of sound for all tissue types, (up to ~50 °C), and thus shift the focus away from the transducer. Fat is the exception, for which the speed of sound drops, resulting in a shift of the focus towards the transducer. The application of such numerical schemes should be based on exposure durations: Hallaj et al. (48) used the method of frozen parameters, with bidirectional coupling between the thermal and acoustic fields, to investigate thermal lensing and its effect on the dose distribution and found that for a 1 MHz single element transducer exposures durations greater than 10 s lead to a shift in the location and change in size of the lesion.

Thermal dose calculations

Arrhenius model & cumulative equivalent minutes

A kinetic model for irreversible damage, Ω, has been derived by Moritz and Henriques (49) (Eq. [9]):

Ω(t)=∫0tAe−EaRT(τ)dτ[9]

In this model, A a constant of proportionality, E_a is the activation energy and R the gas constant.

A closely related (50), but more widely used, measure is the cumulative equivalent minutes formulation discussed above (8). This defines an equivalent time for which a sample is heated with respect to a reference temperature. It is based upon experimental evidence which shows that for cells, both in vivo and in vitro, that there is an exponential relationship between temperature and exposure time to achieve the same effect. Thus, for a given uniform temperature T₁, the heating time t₁ required to produce the same result as heating to a temperature T₂ for a time t₂, is given by (Eq. [10]):

t1=t2R0[10]

where R₀ is (Eq. [11]):

R0=e−EaRT(τ)[11]

and, from the biphasic Arrhenius plot is approximately given by (Eq. [12]):

R0={0T<39∘0.2539∘≤T<43∘0.5T≥43∘[12]

For time-varying temperatures, the equivalent time is obtained by summing contributions from different temperature-time combinations (Eq. [13]):

Tref=∫0t∞R0T−T(t)dt[13]

The most widely used value for defining the threshold for thermal ablation is a CEM₄₃ of 240, which corresponds to raising the temperature to 43 °C for 240 minutes. A reference temperature of 56 °C, has been proposed as more suited to high temperature therapies (51).

For exposures associated with extreme intensities (>20,000 W/cm²), and short exposure times, the time to achieve a CEM₄₃ of 240 may be of order of microseconds (23). The mechanism for cellular damage in such short exposure times is likely to be mechanical damage from boiling. From a practical perspective, such short exposure times may negate the effects of perfusion (52) and tissue motion (53), two significant sources of uncertainty in treatment delivery. These high intensities, may lead to difficulties in predicting lesion formation due to the random nature of cavitation. Thus, while this approach may look attractive in that it leads to reduced treatment times, the ability to cover a large volume accurately and reliably may be challenging.

Intensity-time

An alternative to CEM₄₃, is the intensity-time formulation given by (Eq. [14]):

D=ISPTAtm[14]

where D is a tissue-specific damage threshold and m is a beam- and tissue-specific exponent, derived from computational or experimental data and is typically 0.3-0.8. It has been shown that for clinically relevant HIFU parameters, the cumulative equivalent minutes and intensity time measures are closely matched (54).

Inertial cavitation dose (ICD)

The thermal effects of cavitation can be incorporated as source terms in the bioheat equation and, after computation, will affect the thermal dose (55,56), whereas the non-thermal, that is mechanical, effects of cavitation are less well characterised. The primary mechanism of cavitation is fluid motion due to bubble oscillations which applies stress to cell membranes. As stated earlier, ICD has been defined as an integral of either a portion of, or the entire, received broadband signal. It is strongly dependent on the measurement and signal processing techniques used. For example, a threshold (determined by the signal to noise ratio of the broadband signal) must be specified. Inertial collapse is assumed, which, is itself a source of heating (57). Thus the ICD may not be appropriate for describing the mechanical effects of cavitation. For inertially collapsing bubbles these may be caused by jetting, or for non-inertial oscillations, by micro-streaming (58). A significant challenge in all predictive modelling which includes the effects of cavitation is that nucleation is spatially and temporally stochastic, as is the initial bubble radius of the. One means of resolving this problem is to define a cavitation threshold as a cumulative distribution function empirically, and to average over a large volume, as has been performed for wave propagation through weakly dilute fluid. Jensen et al. (56) investigated the effects of cavitation using passive acoustic mapping to ascertain the location of the cavitation activity and found good agreement between the actual lesion shapes and computational predictions.

Treatment planning/delivery requirements & uncertainties

Image segmentation & tissue characterisation

While image segmentation and registration from pre-treatment data are all well-established for external beam therapies, uniquely, high intensity focused US requires knowledge of the acoustic and thermal properties of all tissue within the propagation path. Tissue geometry comes from applying a threshold to a set of imaging data to delineate tissue types. For example, the Hounsfield unit in each voxel of a CT slice may correlate with the tissue type, and relaxation times may provide this correlation for MR images. As discussed previously, distinguishing different tissue types is important for accurate modelling of the thermal lensing effect. One challenge is that for CT data, automatic contour generation is difficult due to the relatively low contrast between fatty and other soft tissue. This is significant since, the speed of sound for fatty tissue increases with temperature, in contrast to other soft tissues. Once segmented, anatomical boundaries may be computed using an interpolation algorithm, such as a variant of the fast marching cubes method. Accurate knowledge of tissue boundaries is necessary for computing losses from reflection or absorption when there is a significant impedance mismatch, such as exists between bone and soft tissue (59,60). Impedance differences between soft tissues are low, giving losses of only ~1%. Bone may defocus the beam either through diffraction or aberration. It has been shown using finite-element simulations, that when the field is normally incident on bone, the thermal dose at the bone surface can exceed the threshold for necrosis even when the focus is more than 4 cm away (61).

The modality with which pre-treatment images are acquired also plays a significant role in determining which motion compensation strategy is employed. For example, for CT scans there are three techniques which demonstrate the range of motion due to the respiratory cycle: slow, inhale-exhale and four-dimensional CT. Tissue type may also be ascertained from an US image. Typically, five acoustic properties are required for the governing equations: density, speed of sound, nonlinearity and the exponent and coefficient for the attenuation law. The density can be derived from impedance measurements, speed of sound from time of flight, nonlinearity may be measured using finite amplitude insertion methods, and the attenuation coefficient and its exponent can be derived using a substitution method. For thermal properties, the specific heat capacity, thermal conductivity and perfusion terms are required. These can be obtained using thermistors (62) or by matching against experimental data (63) and have been well characterised for a range of tissue types (15).

The thermal effects of flow in small vessels and micro-capillaries are captured by the bulk perfusion term within the bio-heat equation. This may be determined indirectly using least-squares parameter fitting or a reference material. The discrete vascular structure can be derived from ultrafast Doppler imaging.

As mentioned in the section on Thermal models, tissue properties change with temperature. The tissue may also be inhomogeneous. However, many of the governing equations (such as the KZK equation) or numerical methods, (such as the pseudo-spectral and boundary element methods), implicitly assume spatial and temporal homogeneity. Inhomogeneities may be characterised by computing the Nagakami parameter from the backscattered signal (64).

Image registration

Once tissues are demarcated, acoustic properties ascertained and optimal transducer position and settings required to achieve the desired dose computed, the therapy head must be registered with the patient in order to ensure that the dose will be delivered to the correct location.

US-based image registration may be performed by delivering a number of siting shots and determining changes in acoustical properties (65), from acoustic interference patterns (66) or using dual mode US imaging (67). The transducer can be registered with the target using MR (63) or a combination of both (68). In general, there are three approaches to registering the pre-treatment and guidance images:

• Image-to-image registration: this optimizes the pixel-level match between the images;
• Feature-to-feature image registration, in which features, such as large vessels or bones, are extracted from both images, and are then co-registered;
• Model-to-image registration in which features (i.e., “models”) are extracted from one image and then registration occurs by computing the fit of the model to the other image.

The advantages of model-to-image registration are that it only requires extraction from one image (saving time and reducing the chance of error), the images can be from different modalities with the model acting as a converter, and the model can be used to provide spatially and geometrically focused measures of the registration fit, thus speeding up the process. This has been demonstrated in MR-to-US image registration using the boundary of the prostate (69). However, the applicability of US-based registration may be limited because of the presence of ribs and gas.

Motion compensation

There are two types of motion which can affect treatment delivery significantly: that due to respiratory and cardiac cycles, and deformable motion associated with the drift of organs while the patient is in the treatment position. Respiratory motion occurs on a short time scale, and is thus significant for exposures greater than 1 second. Drift occurs on a longer time scale, and so may only be significant for long treatment times. It may also occur during pre-treatment imaging and can potentially lead to registration errors. Cardiac motion is usually ignored for these purposes.

Drift may be accounted for using deformable models, whereas respiratory motion uses either a rigid model, in which the target is simply translated in space, or deformable models.

Respiratory motion affects all organs in the thorax and abdomen—and so can, for example, affect prostate treatments where motion is, on average, 3.3 mm (70). For organs in the upper abdomen, such as the liver, motion may be up to 20 mm (71). Davies et al. (72) showed that the motion of the liver is correlated with the motion of the diaphragm (73) and that, through the course of the breathing cycle, the diaphragm is in the exhale position longer than the inhale position. Lujan et al. (53) defined a periodic but asymmetric model for the rigid motion in a single plane.

From the predicted motion, movement can be tracked using a spirometer, MR (74) or US (75,76). US has the advantages of long penetration depth and real-time frame acquisition. With pre-treatment and intra-operative knowledge of the breathing cycle, a motion compensation strategy may be employed. The easiest ways of achieving this are: breath holding, active breathing control or shallow breathing. These approaches ensure that the target is in the correct location with respect to the pre-treatment data from which the intended dose is computed.

A more advanced technique uses respiratory gating, in which the exposure takes place during a portion of the breathing cycle in which the target is within a desired volume. The position and duration of this ‘gate’ is monitored and triggered with the US exposure.

Tracking target motion, and electronic or mechanical following of the target is, in principle, feasible, but is limited due to a latency associated with computation of the appropriate phases for steering, or with gantry motion. Braunewell et al. have reviewed the techniques and challenges involved in treatment under free breathing (77).

One alternative is to exploit the motion for large volume ablations, allowing the movement to increase the exposed volume (78). This would reduce treatment times, but care is needed to ensure that the correct dose is delivered in each position, and that the lesions completely cover the planned treatment volume.

Treatment strategies and planning

For a given transducer, a measure of dose can be computed from appropriate governing equations and boundary conditions. For effective treatment delivery, constraints, such as the avoidance of exposure to organs at risk (OARs), must be minimized while ensuring that the correct dose is delivered. Thus, treatment planning may involve an optimization scheme for each lesion, defining the position of the transducer and the phase and amplitude for each element, and placement and ordering of lesions. However, in many applications the position of the transducer is not optimized, either because it is fixed (e.g., in transcranial or prostate surgery), or it is determined by the operating clinician.

Focusing strategies

For phased arrays there are a number of techniques for focusing the beam in a given location. These may be used either for electronic steering of the beam, or for ablating at the geometric focus in the presence of obstacles, such as the ribs. The electronic steering capabilities of a transducer are determined by the focusing algorithm and transducer design. Small, sparsely distributed elements on a spherical shell have good steering capability, with a random distribution reducing side-lobes (79-81).

The most basic method for electronic steering is the purely geometric delay-and-sum approach in which the beam is focused by changing the phase from each element to provide constructive interference at the intended target. This method is not computationally demanding, and is straight-forward to implement. It does not, however, allow sparing of OARs.

The most basic technique to avoid OARs is binarised apodisation, also known as adaptive beam-forming. This essentially switches off elements which expose obstacles directly. This can be determined either by ray-tracing or by specifying a threshold intensity for the OAR, computing the contributions from each element, and then determining which elements significantly contribute to the adverse heating. The disadvantage of this method is that, by deactivating some elements, the focal peak intensity may be reduced. There are two ways of overcoming this: increasing the power, or increasing the exposure duration. If additional voltage is supplied to the active elements, the potential for adverse effects associated with high intensities in the propagation path (e.g., skin burns and cavitation) must be addressed. Artefacts associated with motion may be more pronounced with longer exposures.

Time-reversal (82) and phase-conjugation (83,84) exploit the time-reversal symmetry in the linear wave equation in the temporal and frequency domains respectively. Time-reversal methods place a source at the focus, back-propagate towards the surface of the transducer, average the pressures over each element and then convert to surface velocities and drive voltages. Tanter et al. (85) showed that, in a heterogeneous medium, the time-reversal techniques correspond to a spatially and temporally matched filter of the propagation operator, and thus provide an optimal amplitude for each element for a given focal peak intensity. They do not describe the field outside the focus (e.g., the formation of side lobes, or the field at OARs).

The DORT (decomposition of the operator for the time reversal method) technique extends the time-reversal method to minimize the ratio of the SAR for the target and a constrained region (86). This single scalar constraint may limit the applicability of the method, as the resulting field may yield a low focal intensity. Aubry et al. (87) found that time-reversal methods gave little improvement in focal distributions compared to geometric methods such as ray-tracing and binarised apodisation, but spared ribs.

Constrained-optimization can be used to provide the required dose at the target and minimize the dose delivered to OARs. Gélat et al. (88) describe a linear model using a boundary element formulation to minimize the SAR on ribs using a constrained least-squares formulation. Such iterative techniques rely on fast methods to compute the forward model. They may enforce bounds on the constraints using a trust-region algorithm. Two potential short-comings of this method class are that the solution is dependent on a good initial first guess for the phase and amplitudes of the array, and that, without prior knowledge of the Jacobian and derivatives of the propagation operator, as needed for applications with high-intensities and hence nonlinear propagation, the algorithm may be computationally expensive.

Single focus strategies

The sequential deposition of a number of lesions to ablate a planned treatment volume may be achieved using either a single element transducer or a phased array. A phased array can be electronically steered to create multiple lesions without the need for mechanical movement of the transducer, minimizing repositioning errors. If the beam is electronically steered there will be a loss of intensity away from the transducer’s geometric focus and, for most focusing algorithms, enhanced side and grating lobes which will lead to additional heating outside the focus (89). Payne (90) showed that in comparison with mechanical steering, electrical steering led to significant near-field heating.

Because of alterations in the acoustic and thermal properties of the ablated tissue, lesions are placed sequentially in planes starting from the back of the target volume and working towards the transducer. Within each plane, the sequencing of the lesions depends on the extent of the possible electronic steering. It is optimal to place the lesions in such a way as to allow for maximal time for the thermal field to spread. This has the advantage of providing a more uniform temperature distribution within each lesion volume, reducing the probability that heat flow from previous lesions results in asymmetric dose distributions and minimizing the number of exposures need to ablate a given volume, thus reducing treatment time as well as the likelihood alignment errors. To this end some commercial systems execute shots in hexagonal arrays or concentric circles (90) while Salomir et al. used an outward spiralled sequence to exploit heat diffusion (91).

MR thermometry can be used to ensure that the target temperature and thermal dose is delivered (92). Where this is not achieved, exposures can be repeated. However, this strategy is only applicable when real-time thermometry is available; otherwise the lesion size and shape must be predicted using computational or analytical methods (93,94).

For cancer, where complete ablation of the target volume is required, the lesion geometry leads to some overlap between lesions. Assuming the lesions are prolate spheroids the optimal placement can be easily calculated. More advanced techniques use optimization schemes, such as multi-objective evolutionary algorithms which define a surface, (Pareto front) of optimal positions, and durations (95,96). To date, these methods have been developed for RF-ablation, and have been applied to focused-US using a linear approximation of the thermal field generated by a phased array (97). For large or benign targets for which debulking is the goal, complete coverage of the planned treatment volume may not be essential.

Mult-focal strategies

The potential of phased arrays for producing multiple foci has been demonstrated (98). This may reduce total treatment time, and reduce the risk of misalignment of subsequent lesions. Conversely, an initial alignment error will result in a systematic error. Since the power deposited within each sub-volume is less than that using a single focus strategy, exposure durations are longer, and hence may be adversely affected by respiratory motion artefacts. This may be exacerbated since cooling from blood perfusion may be greater for these slightly longer exposure durations.

Conclusions

The many dose descriptors have been described. The challenges associated with reliable, standardised dosimetry in therapeutic US applications have been discussed, and the current state-of-the-art approaches to overcoming the challenges outlined.

Acknowledgments

Funding: David Sinden would like to acknowledge EPSRC grant EP/H046526/1 for generous support and support in part by the European Metrology Research Programme (Joint Research Project HLT03, which is jointly funded by the EMRP participating countries within EURAMET and the European Union) and by the Acoustics and Ionizing Radiation programme of the UK National Measurement Office.

Footnote

Provenance and Peer Review: This article was commissioned by the Guest Editors (Giusi Irma Forte and Giorgio Russo) for the series “High intensity focused ultrasounds” published in Translational Cancer Research. The article has undergone external peer review.

Conflicts of Interest: Both authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.3978/j.issn.2218-676X.2014.10.02). The series “High intensity focused ultrasounds” was commissioned by the editorial office without any funding or sponsorship. The authors have no other conflicts of interest to declare.

Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.

Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.

References

1. Coussios C. High-intensity focused ultrasound: Physical principles and devices. Int J Hyperthermia 2007;23:89-104. [PubMed]
2. Foley JL, Eames M, Snell J, et al. Image-guided focused ultrasound: state of the technology and the challenges that lie ahead. Imaging Med 2013;5:357-70.
3. Larrat B, Pernot M, Aubry JF, et al. MR-guided transcranial brain HIFU in small animal models. Phys Med Biol 2010;55:365. [PubMed]
4. Wu F, Wang ZB, Chen WZ, et al. Extracorporeal focused ultrasound surgery for treatment of human solid carcinomas: early Chinese clinical experience. Ultrasound Med Biol 2004;30:245-60. [PubMed]
5. Gyöngy M, Coussios CC. Passive spatial mapping of inertial cavitation during HIFU exposure. IEEE Trans Biomed Eng 2010;57:48-56. [PubMed]
6. Coussios CC, Roy RA. Applications of acoustics and cavitation to noninvasive therapy and drug delivery. Annu Rev Fluid Mech 2008;40:395-420.
7. Jolesz FA, Hynynen K, McDannold N, et al. Noninvasive thermal ablation of hepatocellular carcinoma by using magnetic resonance imaging-guided focused ultrasound. Gastroenterology 2004;127:S242-7. [PubMed]
8. Sapareto SA, Dewey WC. Thermal dose determination in cancer therapy. Int J Radiat Oncol Biol Phys 1984;10:787-800. [PubMed]
9. Chen WS, Brayman AA, Matula TJ, et al. Inertial cavitation dose and hemolysis produced in vitro with or without Optison. Ultrasound Med Biol 2003;29:725-37. [PubMed]
10. Pierce AD. Acoustics: an Introduction to its Physical Principles and Applications. New York: American Institute of Physics, 1989.
11. Hamilton MF, Blackstock DT. eds. Nonlinear Acoustics. San Diego, CA: Academic Press, 1998.
12. Westervelt PJ. Parametric acoustic array. J Acoust Soc Am 1963;35:535-7.
13. Kreider W, Yuldashev PV, Sapozhnikov OA, et al. Characterization of a multi-element clinical HIFU system using acoustic holography and nonlinear modeling. IEEE Trans Ultrason Ferroelectr Freq Control 2013;60:1683-98. [PubMed]
14. Soneson JE, Myers MR. Gaussian representation of high-intensity focused ultrasound beams. J Acoust Soc Am 2007;122:2526-31. [PubMed]
15. Duck FA. Physical Properties of Tissue: A Comprehensive Reference Book. London: Academic Press, 1990.
16. Treeby BE, Cox BT. Modeling power law absorption and dispersion for acoustic propagation using the fractional Laplacian. J Acoust Soc Am 2010;127:2741-8. [PubMed]
17. Cleveland RO, Hamilton MF, Blackstock DT. Time-domain modeling of finite-amplitude sound in relaxing fluids. J Acoust Soc Am 1996;99:3312-8.
18. Vilensky GG. Thermodynamic theory of nonlinear ultrasound in soft biological tissue. Proc R Soc A 2013;469:20120399
19. Nyborg WL. Heat generation by ultrasound in a relaxing medium. J Acoust Soc Am 1981;70:310-2.
20. Duck FA. A new definition for acoustic dose. In J Phys Conf Ser 2011;12:012006
21. Soneson JE, Myers MR. Thresholds for nonlinear effects in high-intensity focused ultrasound propagation and tissue heating. IEEE Trans Ultrason Ferroelectr Freq Control 2010;57:2450-9. [PubMed]
22. Enflo BO, Hedberg CM. Theory of Nonlinear Acoustics in Fluids. Kluwer Academic Publishers, 2002.
23. Canney MS, Khokhlova VA, Bessonova OV, et al. Shock-induced heating and millisecond boiling in gels and tissue due to high intensity focused ultrasound. Ultrasound Med Biol 2010;36:250-67. [PubMed]
24. Bessonova OV, Khokhlova VA, Canney MS, et al. Focusing of high power ultrasound beams and limiting values of shock wave parameters. Acoust Phys 2009;55:463-76. [PubMed]
25. Holt RG, Roy RA. Measurements of bubble-enhanced heating from focused, MHz-frequency ultrasound in a tissue-mimicking material. Ultrasound Med Biol 2001;27:1399-412. [PubMed]
26. Watkin NA, Rivens IH, ter Haar GR. The intensity dependence of the site of maximal energy deposition in focused ultrasound surgery. Ultrasound Med Biol 1996;22:483-91. [PubMed]
27. Leighton TG. The Acoustic Bubble. London: Academic Press, 1994.
28. Moss WC, Clarke DB, White JW, et al. Hydrodynamic simulations of bubble collapse and picosecond sonoluminescence. Phys Fluids 1994;6:2979-85.
29. Prosperetti A. The thermal behaviour of oscillating gas bubbles. J Fluid Mech 1991;222:587-616.
30. Kamath V, Prosperetti A. Numerical integration methods in gas-bubble dynamics. J Acoust Soc Am 1989;85:1538-48.
31. Flynn HG. Cavitation dynamics: I. A mathematical formulation. J Acoust Soc Am 1975;57:1379-96.
32. Hilgenfeldt S, Lohse D, Zomack M. Sound scattering and localized heat deposition of pulse-driven microbubbles. J Acoust Soc Am 2000;107:3530-9. [PubMed]
33. Pennes HH. Analysis of tissue and arterial blood temperatures in the resting human forearm. J Appl Physiol 1948;1:93-122. [PubMed]
34. Baish JW, Ayyaswamy PS, Foster KR. Heat transport mechanisms in vascular tissues: a model comparison. J Biomech Eng 1986;108:324-31. [PubMed]
35. Wulff W. The energy conservation equation for living tissue. IEEE Trans Biomed Eng 1974;21:494-5.
36. Weinbaum S, Jiji LM. A new simplified equation for the effect of blood flow on local average tissue temperature. J Biomech Eng 1985;107:131-9. [PubMed]
37. Keller KH, Seiler L. An analysis of peripheral heat transfer in man. J Appl Physiol 1971;30:779-86. [PubMed]
38. Charny CK, Levin RL. Bioheat transfer in a branching countercurrent network during hyperthermia. J Biomech Eng 1989;111:263-70. [PubMed]
39. Wissler EH. Comments on the new bioheat equation proposed by Weinbaum and Jiji. J Biomech Eng 1987;109:226-33. [PubMed]
40. Jiji LM, Weinbaum S, Lemons DE. Theory and experiment for the effect of vascular temperature on surface tissue heat transfer -- part II: model formulation and solution. J Biomech Eng 1984;106:331-41. [PubMed]
41. Chen MM, Holmes KR. Microvascular contributions in tissue heat transfer. Ann NY Acad Sci 1980;335:137-50. [PubMed]
42. Deuflhard P, Hochmuth R. Multiscale analysis of thermoregulation in the human microvascular system. Math Meth Appl Sci 2004;27:971-89.
43. Van Leeuwen GM, Kotte A, Raaymakers BW, et al. Temperature simulations in tissue with a realistic computer generated vessel network. Phys Med Biol 2000;45:1035-49. [PubMed]
44. Mann CD, Metcalfe MS, Lloyd DM, et al. The safety and efficacy of ablative techniques adjacent to the hepatic vasculature and biliary system. ANZ J Surg 2010;80:41-9. [PubMed]
45. Payne S, Flanagan R, Pollari M, et al. Image-based multi-scale modelling and validation of radio-frequency ablation in liver tumours. Phil Trans A Math Phys Eng Sci 2011;369:4233-54.
46. Ghoshal G, Luchies AC, Blue JP, et al. Temperature dependent ultrasonic characterization of biological media. J Acoust Soc Am 2011;130:2203-11. [PubMed]
47. Soneson JE. A user-friendly software package for HIFU simulation. In: Ebbini ES. eds. Proceedings: 8th International Symposium on Therapeutic Ultrasound. New York: American Institute of Physics, 2008:165-9.
48. Hallaj IM, Cleveland RO, Hynynen K. Simulations of the thermo-acoustic lens effect during focused ultrasound surgery. J Acoust Soc Am 2001;109:2245-53. [PubMed]
49. Henriques FC Jr, Moritz AR. Studies of thermal injury: I. The conduction of heat to and through skin and the temperatures attained therein. A theoretical and an experimental investigation. Am J Path 1947;23:530. [PubMed]
50. Pearce JA. Relationship between Arrhenius models of thermal damage and the CEM 43 thermal dose. In: Ryan TP. eds. Energy-based Treatment of Tissue and Assessment V. San Jose: Proceedings of SPIE, 2009:718104.
51. Hill CR, Bamber JC, ter Haar GR. Physical Principles of Medical Ultrasonics. Chichester: John Wiley & Sons, 2004.
52. Billard BE, Hynynen K, Roemer RB. Effects of physical parameters on high temperature ultrasound hyperthermia. Ultrasound Med Biol 1990;16:409-20. [PubMed]
53. Lujan AE, Larsen EW, Balter JM, et al. A method for incorporating organ motion due to breathing into 3D dose calculations. Med Phys 1999;26:715-20. [PubMed]
54. Harris GR, Herman BA, Myers MR. A comparison of the thermal-dose equation and the intensity-time Product, It$^m$, for predicting tissue damage thresholds. Ultrasound Med Biol 2011;37:580-6. [PubMed]
55. Chavrier F, Chapelon JY, Gelet A, et al. Modeling of high-intensity focused ultrasound-induced lesions in the presence of cavitation bubbles. J Acoust Soc Am 2000;108:432-40. [PubMed]
56. Jensen CR, Cleveland RO, Coussios CC. Real-time temperature estimation and monitoring of HIFU ablation through a combined modeling and passive acoustic mapping approach. Phys Med Biol 2013;58:5833. [PubMed]
57. Farny CH, Holt RG, Roy RA. The correlation between bubble-enhanced HIFU heating and cavitation power. IEEE Trans Biomed Eng 2010;57:175-84. [PubMed]
58. Prentice P, Cuschieri A, Dholakia K, et al. Membrane disruption by optically controlled microbubble cavitation. Nature Phys 2005;1:107-10.
59. Fan X, Hynynen K. The effect of wave reflection and refraction at soft tissue interfaces during ultrasound hyperthermia treatments. J Acoust Soc Am 1992;91:1727-36. [PubMed]
60. Kossoff G. Basic physics and imaging characteristics of ultrasound. World J Surg 2000;24:134-42. [PubMed]
61. Nell DM, Myers MR. Thermal effects generated by high-intensity focused ultrasound beams at normal incidence to a bone surface. J Acoust Soc Am 2010;127:549-59. [PubMed]
62. Valvano JW, Cochran JR, Diller KR. Thermal conductivity and diffusivity of biomaterials measured with self-heated thermistors. Int J Thermophys 1985;6:301-11.
63. Cornelis F, Grenier N, Moonen CT, et al. In vivo characterization of tissue thermal properties of the kidney during local hyperthermia induced by MR-guided high-intensity focused ultrasound. NMR Biomed 2011;24:799-806. [PubMed]
64. Ho MC, Lee YH, Jeng YM, et al. Relationship between ultrasound backscattered statistics and the concentration of fatty droplets in livers: an animal study. PloS One 2013;8:e63543 [PubMed]
65. Miller NR, Bamber JC, Meaney PM. Fundamental limitations of noninvasive temperature imaging by means of ultrasound echo strain estimation. Ultrasound Med Biol 2002;28:1319-33. [PubMed]
66. Wu CC, Chen CN, Ho MC, et al. Using the acoustic interference pattern to locate the focus of a high-intensity focused ultrasound (HIFU) transducer. Ultrasound Med Biol 2008;34:137-46. [PubMed]
67. Casper AJ, Liu D, Ballard J, et al. Real-time Implementation of a Dual-Mode Ultrasound Array System: In Vivo Results. IEEE Trans Biomed Eng 2013;60:2751-9. [PubMed]
68. de Oliveira PL, de Senneville BD, Dragonu I, et al. Rapid motion correction in MR-guided high-intensity focused ultrasound heating using real-time ultrasound echo information. NMR Biomed 2010;23:1103-8. [PubMed]
69. Hu Y, Ahmed HU, Taylor Z, et al. MR to ultrasound registration for image-guided prostate interventions. Med Image Anal 2012;16:687-703. [PubMed]
70. Malone S, Crook JM, Kendal WS, et al. Respiratory-induced prostate motion: quantification and characterization. Int J Radiat Oncol Biol Phys 2000;48:105-9. [PubMed]
71. Marquet F, Aubry JF, Pernot M, et al. Optimal transcostal high-intensity focused ultrasound with combined real-time 3D movement tracking and correction. Phys Med Biol 2011;56:7061-80. [PubMed]
72. Davies SC, Hill A, Holmes R, et al. Ultrasound quantitation of respiratory organ motion in the upper abdomen. Br J Radiol 1994;67:1096-102. [PubMed]
73. Balter JM, Lam KL, McGinn CJ, et al. Improvement of CT-based treatment-planning models of abdominal targets using static exhale imaging. Int J Radiat Oncol Biol Phys 1998;41:939-43. [PubMed]
74. Ries M, de Senneville BD, Roujol S, et al. Real-time 3D target tracking in MRI guided focused ultrasound ablations in moving tissues. Magn Reson Med 2010;64:1704-12. [PubMed]
75. Pernot M, Tanter M, Fink M. 3-D real-time motion correction in high-intensity focused ultrasound therapy. Ultrasound Med Biol 2004;30:1239-49. [PubMed]
76. Harris EJ, Miller NR, Bamber JC, et al. Speckle tracking in a phantom and feature-based tracking in liver in the presence of respiratory motion using 4D ultrasound. Phys Med Biol 2010;55:3363. [PubMed]
77. Braunewell S, Gunther M, Preusser T. Toward focused ultrasound liver surgery under free breathing. Crit Rev Biomed Eng 2012;40:221-34. [PubMed]
78. Rijkhorst EJ, Rivens I, ter Haar G, et al. Effects of respiratory liver motion on heating for gated and model-based motion-compensated high-intensity focused ultrasound ablation. In: Fichtinger G, Martel A, Peters T. eds. Medical Image Computing and Computer-Assisted Intervention---MICCAI 2011. Berlin, Heidelberg: Springer, 2011:605-12.
79. Gavrilov LR, Hand JW. A theoretical assessment of the relative performance of spherical phased arrays for ultrasound surgery. IEEE Trans Ultrason Ferroelectr Freq Control 2000;47:125-39. [PubMed]
80. Wooh SC, Shi Y. Influence of phased array element size on beam steering behavior. Ultrasonics 1998;36:737-49.
81. Pernot M, Aubry JF, Tanter M, et al. High power transcranial beam steering for ultrasonic brain therapy. Phys Med Biol 2003;48:2577-89. [PubMed]
82. Fink M. Time reversal of ultrasonic fields. I. Basic principles. IEEE Trans Ultrason Ferroelectr Freq Control 1992;39:555-66. [PubMed]
83. Prada C, Manneville S, Spoliansky D, et al. Decomposition of the time reversal operator: Detection and selective focusing on two scatterers. J Acoust Soc Am 1996;99:2067-76.
84. Hynynen K, Jolesz FA. Demonstration of potential noninvasive ultrasound brain therapy through an intact skull. Ultrasound Med Biol 1998;24:275-83. [PubMed]
85. Tanter M, Thomas JL, Fink M. Time reversal and the inverse filter. J Acoust Soc Am 2000;108:223-34. [PubMed]
86. Cochard E, Aubry JF, Tanter M, et al. Adaptive projection method applied to three-dimensional ultrasonic focusing and steering through the ribs. J Acoust Soc Am 2011;130:716-23. [PubMed]
87. Aubry JF, Pernot M, Marquet F, et al. Transcostal high-intensity focused-ultrasound: ex vivo adaptive focusing feasibility study. Phys Med Biol 2008;53:2937-51. [PubMed]
88. Gélat P, ter Haar G, Saffari N. Modelling of the acoustic field of a multi-element HIFU array scattered by human ribs. Phys Med Biol 2011;56:5553-81. [PubMed]
89. Li S, Jackowski M, Dione DP, et al. Refraction corrected transmission ultrasound computed tomography for application in breast imaging. Med Phys 2010;37:2233-46. [PubMed]
90. Payne A, Vyas U, Todd N, et al. The effect of electronically steering a phased array ultrasound transducer on near-field tissue heating. Med Phys 2011;38:4971-81. [PubMed]
91. Salomir R, Palussiere J, Vimeux FC, et al. Local hyperthermia with MR-guided focused ultrasound: Spiral trajectory of the focal point optimized for temperature uniformity in the target region. J Magn Reson Imaging 2000;12:571-83. [PubMed]
92. Köhler MO, Quesson B, Enholm J, et al. Volumetric HIFU ablation under 3D guidance of rapid MRI thermometry. Med Phys 2009;36:3521-35. [PubMed]
93. Filipczyński L, Kujawska T, Wojcik J. Temperature elevation in focused Gaussian ultrasonic beams at various insonation times. Ultrasound Med Biol 1993;19:667-79. [PubMed]
94. Lee KI, Yoon SW. Prediction of the size of a thermal lesion in soft tissue during HIFU treatment. J Korean Phys Soc 2005;47:640.
95. Ren H, Guo W, Sam Ge S, et al. Coverage planning in computer-assisted ablation based on Genetic Algorithm. Comput Biol Med 2014;49:36-45. [PubMed]
96. Shim MB, Kim SJ. Multiobjective optimization technique for treatment planning in HIFU. Ultrasonics Symposium (IUS). 2013 IEEE International. 2013:922-5.
97. Malinen M, Huttunen T, Kaipio JP. Thermal dose optimization method for ultrasound surgery. Phys Med Biol 2003;48:745-62. [PubMed]
98. Ji X, Shen G, Bai J, et al. Multi-element ultrasound phased array applicator for the ablation of deep-seated tissue. J Shanghai Jiaotong Uni 2011;16:55-60.