A chain reaction approach to modelling gene pathways

Background

Cancer can be viewed as a chronic disease that may be influenced by genetic and nutritional factors at various stages in its natural history. The interaction of genes and nutrient components is associated with cancer incidence and tumor behaviour (1-3). It is estimated that one third of all cancer cases may be influenced by diet and associated lifestyle factors, such as food and excess calories for increasing cancer risk (4). On the other hand, many dietary components may have anti-cancer effects by affecting simultaneously multiple cancer processes, such as carcinogen metabolism, hormonal balance, cell signalling, cell-cycle control, and angiogenesis (5). Polyphenols are a group of dietary components found in plants, characterized by the presence of more than one phenol group per molecule. It has been suggested that polyphenols are antioxidants with potential health benefits in reduction of cancer risk (6). Sources of polyphenols include green tea, red wine, soybeans and other fruits and vegetables. To study the interaction of polyphenols on gene expression, the UAB Center for Nutrient-Gene Interaction (CNGI, a NCI funded research program) conducted experiments to examine three dietary polyphenols: genistein from soy, resveratrol from grapes, and epigallocatechin 3-gallate (EGCG) from green tea. A component of this study is to investigate the nutritional modulation of genetic pathways of estrogen synthesis and metabolism using microarray data.

Various pathway databases and methods (e.g., KEGG, GENMAPP, REACTOME, CYTOSCAPE, and BIOCARTA) are available on the internet for pathway analysis (7-12). These curated databases are useful resources to study biological processes, such as the pathways of intermediary metabolism, regulatory pathways, and signal transduction. They also help investigators gain insight into the potential functions of new genes. Since the databases contain massive amounts of information, it becomes challenging for researchers to convert the enormous amount of information into useful knowledge. Many approaches have been developed to provide parsimonious models to analyze gene pathways. For example, MAPPFinder and Pathway-Miner are bioinformatics tools to create global gene expression profiles across biological pathways (13,14). They classify genes by integrating the gene ontology (GO) annotations based on metabolic, cellular and regulatory pathways. Typically, a top list of genes selected by one of these statistical methods is mapped onto pathways with gene product association networks for genes that occur in the pathways. A z-score or the Fisher exact test is then used to test statistical significance of pathways. The pathways can be ranked in accordance with the P values. These tools depict biological interaction among genes and provide insights to study associations of the biological pathways with research outcomes (e.g., disease versus non-disease or treatment versus control). Though these methods provide valuable statistical assessment of gene expression changes, they do not offer the quantitative description of the dynamic relationship and interaction between the genes of interest. Hence, it is difficult to use these methods to disentangle biological processes, and to predict the outcome of gene expression changes due to different initial gene profiles and treatment processes.

The chain reaction model has been widely used in the engineering field to simulate chemical reactions that occur in combustion devices such as jet and rocket engines, etc. (15,16). The chain reaction model contains a set of chemical reactions, where the rate of each reaction was estimated either based on the molecular collision theory of quantum mechanics or from the test data (such as shock tube experiments). In the present study, we propose a chain reaction model to simulate gene pathways as an alternative. The proposed chain reaction model provides a systematic approach for pathway level analyses such that parametric studies of various pathways, selections of genes and nutrient-gene interaction can be performed in an efficient and cost-effective manner. In the proposed model, we use the regulated genes as a set of reacting species and calculate the species changes as the gene expression changes. This approach is applied to a microarray experiment designed to study the nutrient effects on the estrogen synthesis pathway during puberty in which nutrient-, time-, and gene- interactions play a critical role.

Data example

Estrogen synthesis pathway

Figure 1 shows an estrogen synthesis pathway, developed at the Center for Nutrient-Gene Interaction (CNGI) at the University of Alabama at Birmingham (UAB). Estrogens are formed in a series of metabolic channels starting from cholesterol. For example, Desmolase (CYP11a) removes part of the cholesterol side chain to produce the first steroid pregnenolone. Pregnenolone, in turn, undergoes 17α-hydroxylation by CYP17. 17α-hydroxypregnenolone is converted to the adrenal androgen dehydroepiandrosterone (DHEA) by CYP11a. Pregnenolone is also converted to progesterone by 3β-hydroxysteroid dehydrogenase (HSD3b1). Progesterone is converted to testosterone by CYP17, CYP11a and HSD3b1. Aromatase (CYP19) converts testosterone and androstenedione to 17β-estradiol and estrone, respectively. Estrone is reversibly converted to estradiol by 17β-hydroxysteroid dehydrogenase (HSD17b3). Conjugation of estrogens to 3-glucuronides and 3-sulfates is catalyzed by UDP-glucuronosyltransferases (UGTs) and PAPS-sulfotransferases (SULTs), respectively. There are also corresponding hydrolases (glucuronidases and sulfatases) that may selectively release estrogens from conjugates that circulate in the blood.

Figure 1 Estrogen synthesis pathway (http://www.heflingenetics.uab.edu/cngi/esp/pathway.html).

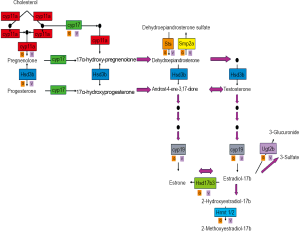
Polyphenols have been shown to inhibit the enzymatic properties of many enzymes in the estrogen synthesis pathway (17,18). However, it is less known about the effects of the polyphenols on the rates of transcription and translation of the genes encoding these enzymes (19). The use of microarray analysis may provide important information about the regulation of these enzymes and identifying gene and protein partners that modulate their activities.

Experimental design

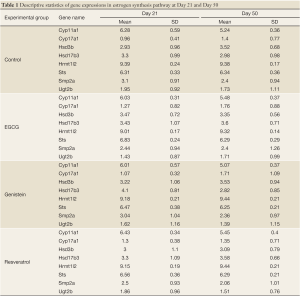
The purpose of this experiment is to examine how the three polyphenols, EGCG, genistein, and resveratrol, affect gene expression in the estrogen synthesis pathway during puberty. The experiment was carried out in a study of 21-day old (puberty) and 50-day old (post-puberty) female Sprague-Dawley rats which were exposed to one of the three polyphenols from birth. At birth, their dams were provided with one of the following: AIN-76A diet (control), AIN-76A diet containing genistein (250 ppm) or resveratrol (1,000 ppm), or AIN-76A diet with EGCG added to the drinking water. The offspring were exposed to one of these nutrients via the dam’s milk and then (after day 21) directly via the diet. The offspring continued to be fed these diets until the time of sacrifice at either day 21 or day 50 - their 4^th mammary gland was removed for the microarray experiment. There were 8-10 rats in each treatment group. Mammary glands were snap-frozen and stored at –80 ^oC for approximately 6 months. The samples were run on the Affymetrix GeneChip^® Rat Genome 230 2.0 (RAE 230) in the UAB Comprehensive Cancer Center Microarray Facility. Data quality was checked using a 2D image plot (20); no problems in these microarrays were found. The Affymetrix gene chip (i.e., RAE 230) contains 31,099 genes and ESTs. Among these genes, there are 8 genes involved in the estrogen synthesis pathway as shown in Table 1. We used the data on these 8 gene expressions to analyze the estrogen synthesis pathway.

Table 1 Descriptive statistics of gene expressions in estrogen synthesis pathway at Day 21 and Day 50
Full table

Statistical and biomechanical approaches

We first performed a statistical analysis to test the time factor on the estrogen synthesis pathway. Since we have interest in this particular estrogen synthesis pathway (not to compare to a known pathway), we used the self-contained gene set methods to evaluate if this pathway is activated from day 21 to day 50. Specifically, two global tests (21-23) were employed to evaluate an overall gene expression change from day 21 to day 50 for each experimental group: a global test with random effects (22) and an ANOVA global test (23). The global test with random effects employs a generalized linear model with a random effect where the random effect is used to examine the time effect from day 21 to day 50. The ANOVA global test is to test the association between gene expressions and the time factor by comparison of linear models through the extra sum of squares principle. Both approaches have been evaluated by Dinu et al. (24) and Fridley et al. (25) and show both have comparable power with similar P values and also have a higher power than the Fisher test. Here we used 0.05 as the P value cut-off for the statistical significance level for both global tests. Univariate analysis for each individual gene was also performed by two-sample t-test to test any expression change from day 21 to day 50. The P value was adjusted for simultaneously multiple testing by the false discovery rate method (26). Then, a chain reaction model was used to simulate the estrogen synthesis pathway. In this model, the regulated genes are treated as a set of chemical species, and the gene change through a conversion process in the pathway is represented by the species change through a reaction channel of the chain reaction model. The chain reaction model involves a set of ordinary differential equations (ODEs) to represent the rates of species change. The reaction rates associated with each reaction channel are used to describe interactions between genes in the pathway. Since numerical errors may occur due to a stiffness problem (e.g., disparate changes of gene expression), we employ an implicit scheme to solve the set of ODEs. The implicit scheme is a numerical algorithm to linearize the gene expression change and approximate the reaction rates using the Taylor series expansion. Employment of the implicit scheme can increase numerical stability and accuracy.

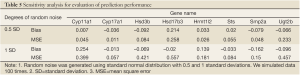
Our hypothesis for this experiment is that the three polyphenols can affect gene expression in the estrogen synthesis pathway during puberty. Thus, we expect gene expression differences between the three treatment groups versus the control group. We first applied the chain reaction model to obtain reaction rates for the control group based on data at day 21 and day 50. A sensitivity study was conducted to evaluate how well the model fits to the control group data at day 50. In the sensitivity analysis, we added a certain degree of normal random noise (0.5 and 1 standard deviations) to expression data at day 21. The chain reaction model then analyzed these noise-added data to obtain a set of predicted expressions. These predicted expressions were compared to the predicted expressions that were estimated based on original data (i.e., no noise added). We computed the bias and mean square error (MSE) for evaluation. A smaller bias and MSE close to 0 indicates robustness of the model. Then the chain reaction model built based on the control group data was used to predict gene expression at day 50 for the three polyphenol groups. When these nutrients affect the estrogen synthesis pathway, we expect discrepancies between observed and expected gene expressions.

Results

Global test approaches to test overall gene expression on the estrogen synthesis pathway

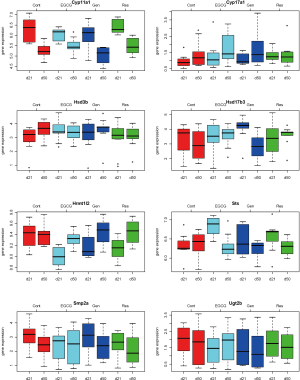
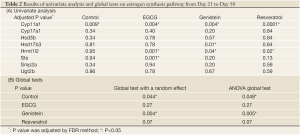
Descriptive statistics and distribution of these 8 gene expressions are displayed in Table 1 and Figure 2. Gene expression change from day 21 to day 50 yielded various patterns. For example in Table 2, gene Cyp11a1 was down-regulated from day 21 to day 50 in the four experimental groups (P=0.009-0.0001). In contrast, gene Hrmt12 had similar expression between day 21 and day 50 in the control group, but was up-regulated from day 21 to day 50 in the other three polyphenol groups (P=0.04-0.001). Statistical data analysis based on the two global tests showed the overall expression changed significantly for the control (P=0.044-0.048) and genistein (P=0.004-0.005) groups based on the P value cutoff of 0.05, but not the EGCG (P=0.27) and resveratrol (P=0.07) groups (Table 3). This observation indicates the estrogen synthesis pathway had been activated from pre- to post- puberty period based on the reference group (i.e., control group). As the nutrients intervened, the pathway was either less activated (e.g., EGCG and resveratrol) or moved to a higher significant activation level (e.g., genistein).

Figure 2 Distribution of gene expressions in estrogen synthesis pathway for the four treatment groups at day 21 and day 50.

Table 2 Results of univariate analysis and global tests on estrogen synthesis pathway from day 21 to day 50
Full table

Table 3 Reaction rates of gene to gene in the estrogen synthesis pathway
Full table

Chain reaction model to evaluate the estrogen synthesis pathway

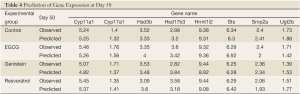
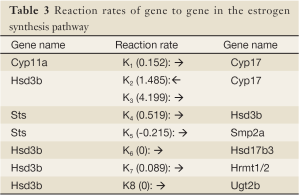
In the present study, we propose an 8-channel chain reaction model, listed in Table 4, to simulate the estrogen synthesis pathway. The 8-channel chain reaction model is selected based on the UAB-CNGI’s estrogen synthesis pathway shown in Figure 1. The reaction rates used in this chain reaction model, estimated based on the mean value of gene expression changes between day 21 and day 50 of the control group, are listed in Table 4. For example, gene Cyp11a regulates gene Cyp17 with a reaction rate, K₁, in the model. Gene Hsd3b co-regulates with gene Cyp17 with a forward rate, K₂, and a backward rate, K₃. Table 4 shows a negative reaction rate from Sts to Smp2a, and two zero rates from Hsd3b to Hsd17b3 and Ugt2b. The zero reaction rates indicate no appreciable gene expression change observed from the microarray data, while the negative reaction rate was caused by opposite trends between the microarray data and the estrogen synthesis pathway. The chain reaction model was employed to analyze the gene expression changes for the control group and 3 treatment groups (EGCG, genistein, and resveratrol), and the predicted gene expressions at Day 50 are shown in Table 5. The difference between the numerical results and the observed data in the control group ranges from –0.18 to 0.22. In the sensitivity analysis, Table 6 shows smaller biases and mean square errors (MSE) for 0.5 and 1 standard deviations (SD) (bias: –0.092~0.214 for 0.5 SD and –0.162~0.254 for 1 SD; MSE: 0.011~0.258 for 0.5 SD and 0.057~0.557 for 1 SD). The sensitivity analysis results indicate that the model is robust to a small amount of random noise (at least within 1 SD). The similarity in the range of difference between the control group in Table 1 and that in the sensitivity analysis result for 1 SD (–0.18~0.22 versus –0.162~0.254) suggests that the model has a good fit for the control group. Moreover, it is expected that there is a discrepancy between the numerical result and the observed results in the treatment groups at Day 50 due to the effect of nutrient diets. The results showed some genes with a large discrepancy between the predicted and observed values, such as Hsd3b and Sts in the EGCG group, and Hsd3b and Hrmt12 in the resveratrol group. These observations suggest nutrient effects in gene expression on this pathway, and, consequently, suggest that the chain reaction model can be estimated for different treatments. Further study can be conducted to obtain the reaction rates for different diet treatment groups and to correlate the nutrient effect on the reaction rates of the estrogen synthesis pathway.

Table 4 Prediction of gene expression at day 50
Full table

Table 5 Sensitivity analysis for evaluation of prediction performance
Full table

Table 6 Numerical order of implicit function
Full table

Discussion

In this paper, we have presented an animal experiment using the microarray technology to study nutrient-gene effects. Since the effects of polyphenols on the estrogen synthesis pathway are not fully understood, this experiment is valuable and allows us to examine how the nutrient-containing diets affect gene expression during puberty. The results may help scientists understand the effect of nutrients on genes and develop effective prevention approaches to reduce cancer risk. To evaluate an overall gene expression change from day 21 to day 50, we employed two global tests to evaluate association of the estrogen synthesis pathway with the time effect (22,23). To study gene-gene interaction, we applied a chain reaction model to simulate the pathway. Although the chain reaction model has been widely used to simulate chemical reactions in the engineering field, this is the first application of this approach to microarray data to the best of our knowledge. The use of the chain reaction model to simulate gene expression changes is a novel application because we translated the gene pathway into a set of chemical reactions in which each reaction channel describes gene-gene interaction in the pathway. Moreover, to address the numerical error issue in the chain reaction model, the implicit scheme was employed to solve the differential equations. The implicit scheme linearizes the gene expression change and approximates the reaction rates with the Taylor series expansions such that numerical stability and accuracy can be increased.

However, due to the limitations of this microarray experiment, the reaction rates used in this study were estimated based on available data at two time slices. Hence, the gene expression change is dependent upon the reaction rates and a linear function of the gene concentrations. This deficiency can be overcome in the future once the test data at various time slices are available to compute the reaction order for each reaction. This additional data will enable us to predict the non-linear gene expression changes throughout puberty, and not just at the end of the puberty cycle. Despite this deficiency, the result of applying the present model to the example data set with a control and 3 three polyphenol treatments provides assessment of the influence of different nutrient treatments on different genes. For example in Table 5, both EGCG and resveratrol groups showed some genes in which the predicted expression greatly differed from the observed value. This observation indicates both nutrients affect the estrogen synthesis pathway, especially for Hsd17b3 and Hrmt12 in the resveratrol group, and Hsd3b and Sts in the EGCG group when compared to the control group. The results are consistent with those of the global tests which yielded different statistically significant levels between the EGCG and the resveratrol groups versus the control group.

Lastly, we would like to point out that the present model is a deterministic approach; thus, it cannot account for the dynamic effects, such as environmental exposure, dietary behavior change, and other unknown factors, which can also contribute to change in expression. Hence, a statistical sampling of the numerical result predicted by the present model is warranted in order to obtain the uncertainty and the margin of errors.

Methods

Chain reaction model

We propose a chain reaction model containing a set of chemical reactions to represent the pathway for the genes of interest, where each reaction channel represents a process of converting a gene to another one in the pathway. In this reaction model, we treat a set of regulated genes as a set of reacting species. By solving the species changes from the reaction model, the change of gene expression can be obtained.

The general form of the chain reaction model (27) can be expressed as

∑j=1ngνij'Φj↔Kb,iKf,i∑j=1ngνij''Φj[1]

Where νij' means stoichiometric coefficients of reactant gene j in reaction channel i, and νij'' represents stoichiometric coefficients of product gene j in reaction channel i. Kf,i and Kb,i are forward and backward rates of gene expression changes in reaction channel i and were estimated based on the gene expression change from day 21 to day 50 (of the control group) obtained from the statistical analysis. Φj indicates the gene j, and ng means the number of genes involved in the chain reaction model. For example, the selected estrogen synthesis pathway contains several genes related to cholesterol, and part of the pathway can be expressed as

{Cyp11aCyp11aHsd3bHsd3bCyp19}forwardgeneexpressionchange→Kf,ibackwardgeneexpressionchangeKb,i←{Cyp17Hsd3bCyp17Cyp19Hsd17b3}[2]

where Φj(j=1,⋯⋯,5) represent Cyp11a, Cyp17, Hsd3b, Cyp19, and Hsd17b3, respectively. In the present chain reaction model, the net expression change of gene j can be calculated from the following equation:

dXjdt=∑i=1nr(νij''−νij')Kf,i∏k=1ng[Xk]rik'+∑i=1nr(νij''−νij')Kb,i∏k=1ng[Xk]rik''=∑i=1nrνij{Kf,i∏k=1ng[Xk]rik'−Kb,i∏k=1ng[Xk]rik''}[3]

where nr is the number of reaction channels in the pathway model, and rik'(rik'') is the power dependence (or so-called reaction order) for reactant (product) gene k in reaction channel i. ^Xk is the concentration of gene k, defined as the ratio of the expression level of gene k to the sum of the expression levels of all the genes considered in this study. It can be seen that the gene expression change not only depends on the reaction rate, but also is a non-linear function of gene concentrations. This is the mathematical model commonly used in the kinetic chemistry for calculating the rate of concentration/fraction change. The use of multiplication is part of the mathematical model to account for the effect of the concentration of all participant genes as reactants. Since each reaction channel can contribute directly or indirectly to the expression change of a given gene, the total expression change rate of a given gene is the sum of the expression change rate associated with each reaction channel. In this preliminary study, the reaction order for all reaction channels is assumed to be unity in order to calculate the reaction rate since we only have data at two time slices (day 21 and day 50).

The chain reaction model involves a set of ordinary differential equations, and may pose a stiffness problem in obtaining a numerical solution (disparate changes of gene expression/species concentration at different time slices) (28-30). Typically, there are two numerical approaches to resolve the stiffness problem: an explicit scheme with a penalty function and an implicit scheme. These two numerical approaches are briefly described as follows.

Explicit scheme for solving the pathway equations

For the explicit scheme, gene concentrations can be calculated from the following equation.

Xjn+1=Xjn+ΔXj=Xjn+Δt(dXjdt)n=Xjn+Δtfjn[4]

Where

fjn=∑i=1nrνij{Kf,i∏k=1ng[Xkn]rik'−Kb,i∏k=1ng[Xkn]rik''}[5]

The superscripts, n and n+1, denote the values at the previous and current time steps, and Δt is the time-step size used for the time integration. The explicit scheme is a very simple method and is computationally efficient because the gene concentration at the next time level can be directly evaluated from the concentration at the previous time level (which is known). However, it may lead to large numerical errors if the reaction model is stiff. A penalty function can be employed to determine the appropriate time step size for integrating the gene expression change, such that the numerical error can be minimized. The penalty function can be expressed as

1Δt=maxj{fjn(ΔXj)a}[6]

Where (ΔXj)a is a pre-set value of the maximum concentration change allowed. Though the penalty function can improve the numerical accuracy, the step size of time integration can be extremely small throughout the time domain, and thus the overall computational time (number of integration steps) can become very long. In addition, the numerical accuracy of this method is highly dependent upon the selected value of maximum concentration change allowed. Hence, users need some experience in order to determine an appropriate value for this parameter.

Implicit scheme for solving the pathway equations

For the implicit scheme, the gene concentrations are calculated based on

Xjn+1=Xjn+ΔXj=Xjn+Δt(dXjdt)n+1=Xjn+Δtfjn+1[7]

where

fjn+1=∑i=1nrνij{Kf,i∏k=1ng[Xkn+1]rik'−Kb,i∏k=1ng[Xkn+1]rik''}[8]

It can be seen that unknowns (Xjn+1,fjn+1) appear on both the right and left hand sides of the equations; hence, the set of equations cannot be solved directly. Taylor’s series expansion was employed to linearize the production/dissipation rate term fjn+1, and can be expressed as

fjn+1=fjn+∑k=1ng(∂fj∂Xk)n(Xkn+1−Xkn)=fjn+∑k=1ng(∂fj∂Xk)nΔXkn+1[9]

Using different approximations to achieve various orders of numerical accuracy, a general form of a set of algebraic equations can be obtained as

ΔXjn+1−∑k=1ngAj,kΔXkn+1=C3fjnorBY=S[10]

Where

Aj,k=C1Dj,k+C2Dj,k2andDj,k=(∂fj∂Xk)n[11]

B=[1−A1,1−A1,2⋯−A1,ng−1−A1,ng−A2,11−A2,2⋯−A2,ng−1−A2,ng⋮⋮⋱⋮⋮−Ang−1,1−Ang−1,2⋯1−Ang−1,ng−1−Ang−1,ng−Ang,1−Ang,2⋯−Ang,ng−11−Ang,ng]Y={ΔX1n+1ΔX2n+1⋮ΔXng−1n+1ΔXngn+1};S=C3{f1nf2n⋮fng−1nfngn}[12]

The values of C₁, C₂, and C₃ for different orders of numerical accuracy are listed in Table 6, respectively.

Though the implicit methods require solving the matrix, the possible numerical error due the stiffness problem can be greatly reduced. In addition, users do not have to select an ad-hoc value for the allowable maximum gene changes. Therefore, we employed the implicit scheme to solve the chain reaction model of the pathway. The numerical accuracy of the employed implicit scheme has been demonstrated by solving a much stiffer chemical reaction such as hydrogen-oxygen and hydrocarbon-oxygen reactions, and the result was published previously (15,16).

Acknowledgments

We thank Mrs. Connie Pitts for secretarial assistance.

Funding: This work was supported by grants from the National Cancer Institute (5P30 CA-13148, 1P50 CA89019, and 1U54 CA100949).

Footnote

Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.3978/j.issn.2218-676X.2012.05.06). DTC serves as an unpaid editorial board member of Translational Cancer Research. The other authors have no conflicts of interest to declare.

Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.

Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.

References

1. Available online: http://www.heflingenetics.uab.edu/cngi/esp/pathway.html
2. Henning SM, Niu Y, Lee NH, et al. Bioavailability and antioxidant activity of tea flavanols after consumption of green tea, black tea, or a green tea extract supplement. Am J Clin Nutr 2004;80:1558-64. [PubMed]
3. Davis CD, Milner J. Frontiers in nutrigenomics, proteomics, metabolomics and cancer prevention. Mutat Res 2004;551:51-64. [PubMed]
4. Go VL, Nguyen CT, Harris DM, et al. Nutrient-gene interaction: metabolic genotype-phenotype relationship. J Nutr 2005;135:3016S-20S. [PubMed]
5. Surh YJ. Cancer chemoprevention with dietary phytochemicals. Nat Rev Cancer 2003;3:768-80. [PubMed]
6. Arts IC, Hollman PC. Polyphenols and disease risk in epidemiologic studies. Am J Clin Nutr 2005;81:317S-25S. [PubMed]
7. Dahlquist KD, Salomonis N, Vranizan K, et al. GenMAPP, a new tool for viewing and analyzing microarray data on biological pathways. Nat Genet 2002;31:19-20. [PubMed]
8. Joshi-Tope G, Gillespie M, Vastrik I, et al. Reactome: a knowledgebase of biological pathways. Nucleic Acids Res 2005;33:D428-32. [PubMed]
9. Kanehisa M, Goto S, Hattori M, et al. From genomics to chemical genomics: new developments in KEGG. Nucleic Acids Res 2006;34:D354-7. [PubMed]
10. Kanehisa M, Goto S, Kawashima S, et al. The KEGG resource for deciphering the genome. Nucleic Acids Res 2004;32:D277-80. [PubMed]
11. Shannon P, Markiel A, Ozier O, et al. Cytoscape: a software environment for integrated models of biomolecular interaction networks. Genome Res 2003;13:2498-504. [PubMed]
12. Available online: http://www.biocarta.com
13. Doniger SW, Salomonis N, Dahlquist KD, et al. MAPPFinder: using Gene Ontology and GenMAPP to create a global gene-expression profile from microarray data. Genome Biol 2003;4:R7. [PubMed]
14. Pandey R, Guru RK, Mount DW. Pathway Miner: extracting gene association networks from molecular pathways for predicting the biological significance of gene expression microarray data. Bioinformatics 2004;20:2156-8. [PubMed]
15. Cheng GC, Anderson P, Farmer RC. Development of CFD model for simulating gas/liquid injectors in rocket engine. In. 33rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference 1997:97-3228.
16. Cheng GC, Farmer RC, Chen YS. Numerical study of turbulent flows with compressibility effect and chemical reactions. In. 6th AIAA/ASME Joint Thermophysics and Heat Transfer Conference 1994:94-2026.
17. Flynn KM, Ferguson SA, Delclos KB, et al. Effects of genistein exposure on sexually dimorphic behaviors in rats. Toxicological sciences: an official journal of the Society of Toxicology 2000;55:311-9.
18. Wang ZY, Khan WA, Bickers DR, et al. Protection against polycyclic aromatic hydrocarbon-induced skin tumor initiation in mice by green tea polyphenols. Carcinogenesis 1989;10:411-5. [PubMed]
19. Mentor-Marcel R, Lamartiniere CA, Eltoum IE, et al. Genistein in the diet reduces the incidence of poorly differentiated prostatic adenocarcinoma in transgenic mice (TRAMP). Cancer Res 2001;61:6777-82. [PubMed]
20. Chen DT. A graphical approach for quality control of oligonucleotide array data. J Biopharm Stat 2004;14:591-606. [PubMed]
21. Goeman JJ, Oosting J, Cleton-Jansen AM, et al. Testing association of a pathway with survival using gene expression data. Bioinformatics 2005;21:1950-7. [PubMed]
22. Goeman JJ, van de Geer SA, de Kort F, et al. A global test for groups of genes: testing association with a clinical outcome. Bioinformatics 2004;20:93-9. [PubMed]
23. Hummel M, Meister R, Mansmann U. GlobalANCOVA: exploration and assessment of gene group effects. Bioinformatics 2008;24:78-85. [PubMed]
24. Dinu I, Potter JD, Mueller T, et al. Gene-set analysis and reduction. Brief Bioinform 2009;10:24-34. [PubMed]
25. Fridley BL, Jenkins GD, Biernacka JM. Self-contained gene-set analysis of expression data: an evaluation of existing and novel methods. PLoS ONE 2010;5:e12693 [PubMed]
26. Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J R Stat Soc B 1995;57:289-300.
27. Farmer RC, Cheng GC, Chen Y-S, et al. Computational Transport Phenomena for Engineering Analyses. In: CRC Press, Taylor & Francis Group; 2009.
28. Curtiss CF, Hirschfelder J. Integration of stiff equations. Proc Natl Acad Sci USA 1952;38:235. [PubMed]
29. DeGroat J, Abbett M. A computation of one-dimensional combustion of methane. AIAA J 1965;3:381-3.
30. Moretti G. A new technique for the numerical analysis of nonequilibrium flows. AIAA J 1965;3:223-9.