Proton therapy dose calculations on GPU: advances and challenges

Proton therapy can allow higher dose conformality compared to conventional radiation therapy. Radiation dose calculation has an integral role in the success of proton radiotherapy. An ideal dose calculation method should be both accurate and efficient. Over the years, a number of dose calculation methods have been developed. To overcome the high computational burden of these algorithms, or to further speed them up for advanced applications, e.g., inverse treatment planning, graphics processing units (GPUs) have recently been employed to accelerate the proton dose calculation process. In this paper, we will review a set of available GPU-based proton dose calculation algorithms including a pencil-beam method, a simplified Monte Carlo (MC) simulation method, a track-repeating MC method, and a full MC simulation method. The advantages and limitations of these methods will be discussed. We will also propose a dose calculation method via solving the Boltzmann transport equations, which is expected to be of the same level of accuracy as a MC method but could be more efficient on GPU.

Introduction

Cancer radiation therapy aims at delivering a prescribed radiation dose to cancerous targets, while sparing the surrounding organs at risk and normal tissues by conventional high-energy X-ray beams or by particle beams such as protons. A proton beam, due to its unique way of depositing dose, has clinical advantages over X-ray beams. As a proton beam travels through a patient, it forms a sharp maximum, the Bragg peak (1,2), at the end of its range as a result of the phenomenon that the energy deposition increases with penetration depth. One can control the peak location by varying the beam energy, and then assemble a set of peaks to form a plateau called Spread-Out Bragg Peak (SOBP). Favorable dose distributions with a relatively homogeneous region and steep dose fall-offs can therefore be easily achieved, resulting in greater dose localization than can be produced by conventional photon beams. Hence, dose escalation can be performed while mitigating radiation toxicity in surrounding normal tissues.

Dose calculation plays a critical role in a proton therapy treatment. Generally speaking, a clinically desirable dose engine should attain the following features. First, it has to be accurate. The sharp dose fall-off at the distal end of a proton beam makes the dose distribution extremely sensitive to dose calculation error. Inaccuracies in the calculations of proton penetration can easily shift the SOBP, which leads to under coverage of the target and over dose to surrounding health tissues. It has been reported that the proton range uncertainty due to dose calculation methods alone is about 2-3%. This estimated error excludes uncertainties in other practical issues encountered in dose calculation such as CT image calibration and conversion to tissue properties. Efficiency is another crucial requirement for proton dose calculation. In the time-critical clinical environment, not only does a fast dose engine ensure a smooth workflow, but also it offers planners opportunities to fine tune treatment parameters to select the most beneficial set of parameters for each individual patient. Efficient and accurate dose calculations have become even more critical lately in those novel technologies where repeated dose calculations are necessary, for instance, in intensity-modulated proton therapy (3,4) and 4D treatment planning (5,6).

Yet, it is quite difficult, if not impossible, to develop dose calculation techniques that meet both of these two requirements. In practice, it usually means prolonged computation time, if one prefers a highly accurate dose calculation result. One example is the Monte Carlo (MC) simulation method, where the accuracy is ensured by faithful simulation of particle transport. The computation time required to attain a level of acceptable accuracy prohibits its applications in clinical practice. It has been reported that it takes a few hours to compute the dose for a patient with 2.5% relative uncertainty using the MC method on a typical computer (7). In another calculation approach where computation time is also critical, pencil beam (PB) models can be used in conjunction with empirical data tables (8-10). The accuracy of PB methods is, however, compromised by the simplifying assumptions built into them. To date, there is no dose calculation engine that attains the accuracy and speed required for the clinical setting. Hence, despite the apparent advantages of proton therapy, its potential is highly limited by unsatisfactory dose calculation algorithms, potentially making the treatment delivered to patients suboptimal.

One practical approach to achieve the combined accuracy and efficiency is to utilize more powerful computational hardware. Recently, the development of general-purpose graphics processing unit (GPU) hardware and software has been rapidly progressing for the purposes of massively parallel scientific computing, resulting in enormous, affordable, and readily accessible computational power that are particularly suitable for routine clinical uses. Specific to dose calculation problems in radiotherapy, GPU has been utilized to speed up pencil-beam algorithms (11,12), superposition-convolution algorithms (13,14), and MC simulations (15-22). With these efforts, the calculation time of MC-based proton dose calculation has been greatly shortened. This also indicates that it is affordable to consider more complex physics in the dose calculation process, resulting in considerably enhanced calculation accuracy, especially in cases with complicated geometry and large heterogeneities.

In this paper, we will review a set of current state-of-the-art GPU-based dose calculation methods with emphases on their implementations, current status, and potential improvements. A promising algorithm based on the Boltzmann transport equation will also be proposed. The rest of this paper is organized as follows: Section 2 will give a brief introduction about GPUs and Section 3 will discuss three groups of GPU-based dose calculation algorithms, Section 4 will conclude the paper with discussions.

Graphics processing unit

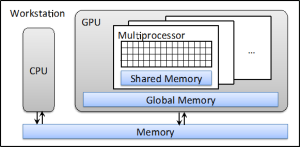
A graphics processing unit (GPU) is a specialized hardware in a computer system designed to accelerate the processing of graphics information. In a modern desktop workstation, it is usually in the form of a separate card plugged onto the motherboard. The advantages of a GPU over a conventional computational hardware, e.g., central processing unit (CPU), come from its large number of processing units. For instance, an NVIDIA Tesla C2050 GPU that is manufactured specifically for scientific computing purposes contains 448 thread processors. Although the clock speed of each of them is relatively lower than that of a CPU, the combined processing power of them is over 1 Tflops, much larger than what can be achieved by a CPU. All of these GPU threads share the use of a common piece of memory space called global memory, and some of them are grouped together, share the so-called shared memory, which offers a much higher speed than the global memory. Figure 1 depicts the structure of a typical computer workstation with a GPU installed.

Figure 1 Illustration of the structure of a computer workstation that contains a GPU.

GPU follows a SIMD (single instruction multiple data) (23) design in its execution scheme. As such, a GPU executes a program in groups of 32 parallel threads termed warps. If the paths for threads within a warp diverge due to, e.g., some if-else statements, the warp serially executes one thread at a time, while putting all other threads in an idle state. Thus, high computation efficiency is only achieved when all threads in a warp process together along a same execution path. Under this structure, some operations are essentially GPU-friendly while others are not. An example in this category include vector and matrix operations, as different GPU thread can process different matrix entries in the same operational fashion but with different data. It is for this reason that pencil-beam based dose calculation algorithms are suitable for GPU, as the calculation algorithms can be mathematically formulated as matrix-vector operations. In contrast, it is quite difficult to achieve high speed-up factors for MC dose calculations on a GPU, because the work paths on different threads are statistically independent and can be very different in an MC calculation.

Proton dose calculations on GPU

Pencil-beam method

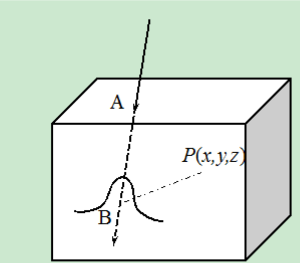
Pencil-beam dose calculation algorithm for proton therapy has a long history (8-10,12). Because of its simplicity of calculation scheme and acceptable accuracy in most clinical settings, this method has been widely utilized in routine clinical applications for treatment planning purposes. The dose calculation algorithm starts from the assumption regarding the dose distribution of a pencil-beam. Take a commonly used Gaussian function kernel as an example; for a pencil-beam irradiated along the axis, the dose deposited at the point (x, y, z) can be written as

K(x,y,z)=p(deff)(SSD+deffz)2G(x,y,z),[1]

where p(deff) is the depth dose distribution of a pencil-beam, which is usually determined from experiments in a water medium and deff is the water-equivalent length from the phantom surface A to the point B on the pencil-beam axis, see Figure 2. The second term corresponds to the inverse square correction, while the third one describes the dose spread out inside the plane perpendicular to the z axis and is empirically taken as a Gaussian function in this model

G(x,y,z)=12πσ(z)exp[−x2+y22σ2(z)].[2]

Figure 2 Illustration of the pencil-beam algorithm.

Note that the amount of beam spread is characterized by the quantity σ(z), which is an increasing function of the depth z. Physically, this spread is due to the lateral scattering during the proton propagation. In practice, an empirical function form is usually employed which combines the contributions from two sources, namely the proton beam nozzle and the patient (9). Finally, with the dose deposition for a single proton beam given in Eq. [1], the dose distribution for a broad beam can be expressed as a summation over all the pencil-beams as

d(x,y,z)=∫∫Σdx′dy′T(x′,y′)K(x−x′,y−y′,z),[3]

Where T(x,y) parameterizes the pencil-beam intensity and the integral is carried out over an area Σ on which all the pencil beams pass through.

The computations can be decomposed into the following/g steps. First, a broad beam is divided into a set of pencil beams and ray-tracing calculation is performed along the central axis of each pencil beam to determine the water equivalent depth deff. Next, for each voxel, the dose is equal to the summation over the contributions from all the pencil beams, which can be easily evaluated by using Eq. [1]. In this step, the corresponding quantities such as p(deff) and σ(z) are determined based on available data tables. It is straightforward to parallelize both of these two steps. The first one can be parallelized with each GPU thread responsible for a pencil beam, while the second step is accomplished by assigning each voxel to a thread. Because of the largely available number of GPU thread processors, the computational efficiency is extremely high for this method. For instance, it has been reported that the computational time is less than 1 second for most of the cases tested (12) on an NVIDIA Geforce GTX 480 GPU.

Apart from the apparent advantages of computational efficiency of this pencil-beam approach, it also provides dose distributions from each single pencil beam. Such important information is of critical importance for many clinical applications such as intensity-modulated proton therapy, where the intensity of each pencil beam is optimized to yield a desired dose distribution. It is for these reasons that pencil beam algorithms are currently widely employed in routine clinic for proton therapy treatment planning.

Yet, it should be noted that this method is only a temporary solution for proton dose calculation due to its questionable accuracy in some cases. In fact, the Eq. [3] is only a phenomenological description about how dose is deposited to the patient, and the physics of proton transport is missing here. In some cases with complicated geometry and/or large amount of tissue heterogeneity, the accuracy of this method could be significantly reduced. Even though a variety of pencil-beam models have been proposed over the years, it has been pointed out that no single pencil-beam model can result in correct dose in every situation (24). Another limiting factor of this model is the associated difficulties in commissioning, where the empirical data p(deff) and σ(z) must be determined. In a typical approach, this commissioning step is treated as an optimization problem in which these data are determined by numerical algorithms so that the calculated dose matches measurements in some simple cases, e.g. water. This is a very tedious task, as σ(z) goes to the denominator in an exponential term in Eq. [2] and a highly nonlinear system needs to be solved.

Monte Carlo method

Monte Carlo (MC) simulation is commonly regarded as the most accurate method for radiotherapy dose calculation due to its capability of faithfully transporting a particle according to the underlying physics and modeling the patient geometry and material properties. It has been demonstrated that the use of MC in proton therapy could lead to a significant reduction in treatment planning margins (25). As a statistical method, the precision of an MC dose calculation is governed by the total number of particles simulated and an enormously large number of particles are usually required. Hence, despite the great efforts devoted to accelerating the MC dose calculation process, such as using large-scale computational hardware and developing simplified algorithms (26-29), this method is still mainly applied for re-calculating existing treatment plans for research studies or for secondary dosimetric calculations that are not time sensitive. The unsatisfactory efficiency also impedes the progresses of advanced treatment techniques in proton therapy, such as MC-based treatment planning and adaptive proton radiotherapy. Recently, with the aim of increasing the efficiency of MC dose calculations, a number of research groups have developed a few packages on GPU. Here, three representative types of GPU-based MC methods will be discussed.

Simplified Monte Carlo simulation

The first approach to alleviate the high computational burden in a MC simulation is to employ some simplified physics. Motivited by this idea, Kohno et al. (27) developed a simplified MC method (SMC) for proton dose calculations. It was later implemented it on a GPU platform (19) and used for treatment planning. The SMC method begins by setting each individual proton with a location, a velocity direction, and a residual range in water. Once the transport starts, the proton travels through the voxelized geometry. At each voxel, there are two effects modeled. First, the proton’s residual range is reduced according to the local material property and a corresponding amount of energy is deposited to the voxel, which is determined by a water equivalent model (30) based on the measured depth-dose distribution in water. Second, multiple Coulomb scattering of the proton is modeled, where the scattered angles are sampled from a normal distribution with a standard deviation given by Highland formula (31). This model contains a much simplified proton transport physics compared to what happens in reality. For example, as opposed to determining dose deposition at each voxel according the actual physical interaction process, it is determined using the measured depth-dose distribution in water. This is essentially an effective model, as those real interactions occurring locally at the voxel are phenomenologically described and the net effect in terms of dose deposition is captured. This avoidance of sampling detailed interaction processes preserves the accuracy to an acceptable extent while greatly simplifies the model and increases the efficiency.

In terms of GPU implementation, this SMC algorithm is compatible with GPU’s SIMD structure. This is because the proton transport process described above can be carried out by each GPU thread independently, where all of the threads repeated perform the same instructions but using different data according the current proton status. Moreover, high speed shared memory is utilized in the implementation. In terms of the achieved efficiency, a speed-up factor of 12-16 compared to CPU implementation has been observed in real clinical cases. Regarding the absolute dose calculation time, it was found that with 9-67 seconds, one can attain a clinically acceptable uncertainty on an NVIDIA Tesla C2050 GPU.

Track-repeating Monte Carlo simulation

Track-repeating is a variance technique utilized in MC simulations for dose calculations. In the context of proton transport, this technique was first utilized by Li et al. (26) and then recently implemented on a GPU platform (18,28). In this method, a database of proton transport histories is first generated in a homogeneous water phantom using an accurate MC code such as GEANT4 (32). Each particle trajectory consists of a set of steps, and for each step, the direction, step length, and energy loss are stored. The computational load for this step is not a practical issue, as this database preparation step is only performed once and the generated database will be repeated used later on. For a patient case, the track-repeating MC calculates dose distributions by repeating appropriate proton tracks in the database. As such, it first generates a proton at the surface of the phantom and selects a track in the database corresponding to this proton. The proton is then transported as if it follows this assigned track inside the patient. The underlying assumption is that the random numbers generated while transporting this proton are identical to what occurred when generating the track in the database, and hence leading to an identical trajectory. To account for the tissue heterogeneity of the patient, each step length and the scattering angle within this track is scaled according to the local properties of the non-water medium. The dose depositions recorded for the steps are added to the corresponding voxels.

This method is computationally efficient for two reasons. Regarding the transport process, it avoids the sampling of physical interactions on the fly. Hence, the majority of the computational burden in a MC simulation is eliminated. Yet, as the tracks are pre-generated by an accurate MC simulation, this simplification does not result in a significant degradation of dose calculation accuracy. In validation studies (14,24), it was discovered that the dosimetric results of this method agree with those from a full MC simulation using GEANT4 within 1% discrepancy. Second, regarding its advantages in the GPU context, this method is quite GPU-friendly. Each GPU thread essentially performs the same operations at all the time. Therefore, the full GPU power can be employed, leading to a high computational efficiency. The aforementioned 1% accuracy can be accomplished in less than 1 minute with a dual GPU system equipped with Geforce GTX 295 GPUs. A speedup of a factor of 75.5 with respect to the same CPU-based implementation has been reported.

Full Monte Carlo simulation

The accuracies achieved in the two MC codes discussed in Sections 3.2.1 and 3.2.2 is found to be sufficient for clinical applications in most of the cases. Yet, in those cases with unique situations of heterogeneity, a full MC simulation is still desired. Examples include those places where charge particle disequilibrium occurs or at interfaces between two mediums with quite distinct properties. It is challenging to develop a full MC dose calculation package for proton therapy on GPU. First, protons interact with human tissue through various types of interactions, but not all of them are necessary for dose calculations. Careful investigations with respect to how much detail one should include in the simulations are needed in order to balance accuracy and efficiency. Second, from the computational point of view, the inherent conflict between the GPU’s SIMD processing scheme and the stochastic nature of a MC process poses a big challenge (16,17,33).

Only until recently has a full MC simulation package, gPMC, been developed for proton dose calculation on GPU (20). The distinction between this package and the above-mentioned packages is that it tracks a proton according to the realistic physical process on the fly. Specifically, proton propagation is modeled by a Class II condensed history simulation scheme using the continuous slowing down approximation. The proton is transported in a step-by-step fashion until its energy is below a user-defined cut-off energy or it exits the phantom region, where each step terminates at an interaction point, a voxel boundary, or a upper bound set by the user. Ionization, elastic, and inelastic proton nucleus interactions are considered. Energy straggling and multiple scattering are also modeled. As for nuclear interactions, gPMC follows an empirical strategy invented by Fippel and Soukup (29). Only proton-proton elastic interactions, proton-oxygen elastic, and inelastic interactions are included. The secondary protons generated in the proton-proton elastic interactions and in the proton-oxygen inelastic interactions are tracked by the same proton transport physics mentioned above. All other heavy charged particles are terminated and their energies are locally deposited. Charge-neutral particles produced in the proton-oxygen inelastic events are simply neglected.

gPMC performs dose calculations in a batched fashion. In each batch, a certain number of source protons and the produced secondary protons are transported and dose depositions are recorded. The results from different batches are then analyzed statistically to obtain the average dose to each voxel and the corresponding uncertainties. To further ensure the computational efficiency, a high-performance pseudo-random number generator CURAND developed by NVIDIA is utilized, which offers simple and efficient generation of high-quality pseudo-random numbers using the XORWOW algorithm. GPU texture memory is also employed to support hardware-based interpolation on the cross section and stopping power data.

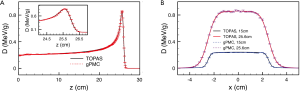
The success of gPMC has been established by comparing the dose calculation results with those from TOPAS/Geant4 (34), a golden standard MC simulation package. For a set of cases ranging from homogeneous and inhomogeneous phantoms to a patient case, sufficient agreements between gPMC and TOPAS/Geant4 are observed. Specifically, gamma passing rate for a 2%/2 mm criterion is over 98.7% in the region with dose greater than 10% maximum dose in all cases. A comparison of the dose distributions computed by the two algorithms is shown in Figure 3. With respect to the efficiency, it takes only 6-22 sec to simulate 10 million source protons to yield ~1% relative statistical uncertainty on an NVIDIA C2050 GPU card, depending on the phantoms and the energy. This is an extremely high efficiency compared to the computational time of tens of CPU hours for TOPAS/Geant4.

Figure 3 Depth dose curves (A) and lateral profiles (B) for a water phantom with a 200 MeV source, respectively. Inserts are zoomed-in views of the depth curves near the Bragg peak.

One interesting issue discussed by Jia et al. is that there exists a memory writing conflict problem when using GPU for MC dose calculations (20). Because of the shared-memory programming mode of a GPU, a single dose counter allocated in the GPU’s global memory is responsible for recording the dose information deduced by all GPU threads. When two threads happen to deposit dose information to a voxel at the same time, a memory writing conflict occurs and the energy deposition has to be serialized in order to obtain correct results. In practice, gPMC uses an atomic float addition function to serialize the dose addition. This function is called atomic in that, once a GPU thread is writing to a memory address, it takes the full control and no other threads can interfere with this process. However, this serialization apparently counteracts the available parallel processing power of a GPU. A higher frequency of conflict occurrences indicates a greater reduction of the overall efficiency. Even though this memory writing conflict occurs also in x-ray beam dose calculations (15,16), it is, exacerbated in the context of proton beams. This is because protons travel almost along a straight line and a parading column of protons in a beam, especially in a small-size beam, marches in almost locked step with each other leading to a high possibility of memory writing conflicts. To date, there is no practical solution to this problem and careful investigations on this issue are needed.

Boltzmann transport

An alternative for proton dose calculations is to deterministically solve the Boltzmann transport equation (BTE) (35,36), which describes particle transport by a partial-differential-integral-equation formulated in phase space. It has been demonstrated that deterministic methods can compete with MC in terms of accuracy (37) as the latter is essentially a way of solving the BTE by statistical methods. Because of the absence of random fluctuations, the deterministic approach is well suited for evaluating small dose variations in a typical treatment. Moreover, this approach leverages the use of mature numerical algorithms ensuring both accuracy and efficiency. In the past, dose calculation packages via this deterministic approach for conventional high-energy photon therapy have been developed and applied in routine clinical practice (35,38-40). Its acceptance as an integral part of photon therapy clearly indicates its potential in proton therapy. Yet, the use of BTE for proton dose calculation is still under investigation. In the following we outline the use of BTE in proton dose calculations.

Let us consider a bounded region X, which contains a voxelized patient anatomy. The proton dose calculation problem is to compute the radiation dose deposited into each voxel under a proton beam configuration defined in a treatment plan. The beam configuration is characterized by the proton fluence at the boundary ∂X. Let us further denote a proton fluence at location x with unit velocity direction Ω and energy E as ψ(E,Ω,x). Under the continuous slowing down approximation, the steady state BTE that administers the proton fluence ψ can be expressed as (41,42)

Ω⋅∇ψ(E,Ω,x)+σ(E,x)ψ=QSca(E,Ω,x)+σS(E,x)ψ∂E,ψ(E,Ω,x)=ψ¯(E,Ω),n⋅Ω<0,x∈∂X,[4]

where ψ¯(E,Ω), the Dirichlet condition of ψ on the inflow surface, is the specification of the proton fluence at the boundary ∂X, and n is the unit normal of the boundary surface. S(E,x) and σ(E,x) are the total stopping power and total cross section in the medium at x at energy E, respectively. The scattering term QSca(E,Ω,x) is given by

QSca(E,Ω,x)=∫0∞dE′∫Ω′∈S2dΩ′σ(E,E′;Ω⋅Ω′;x)ψ(E′,Ω′,x),[5]

where σ(E,E′;Ω⋅Ω′;x) is the differential cross section for the medium at x. Once the BTE is solved for ψ, a radiological quantity of interest such as dose at location x can be obtained by:

D(x)=1ρ(x)∫0∞dE∫Ω∈S2dΩσp(E,x)ψ(E,Ω,x)[6]

Here, σp(E,x) is the cross section corresponding to the quantity of interest and ρ(x) is the density.

The total cross section σ(E,x) is the sum of all the cross sections for all interactions considered. In the energy range up to a few hundred MeV for proton therapy, ionizing collisions are the most important interactions in this model. Although nuclear reactions are significant for a typical clinical proton beam, a nuclear reaction of a proton within a material can be approximately treated as if the reaction was with water, as human tissue is approximately water-equivalent. Therefore, only proton-proton elastic scattering, proton-oxygen elastic scattering and proton-oxygen scattering are needed.

The BTE in Eq. [4] is too complicated to have a closed-form analytical solution. Yet, it is possible to solve it numerically. A typical approach is to employ the so called multi-group discretization of E and the discrete-ordinate discretization of Ω, yielding:

Ωd⋅∇ψg,d(x)+σg(x)ψg,d(x)=Qg,dSca(x)+Sg+1.2ψg+1,d−Sg−1/2ψg,dΔEgψg,d(x)=ψ¯g,d,n⋅Ωd<0,x∈∂X.[7]

where the indices d and are used to label the descritized angular direction Ω and energy E, respectively. A forward finite difference scheme can be used to approximate the stopping power term ∂(Sψ)/∂E, which is mathematically proven to be numerically stable. A further discretization of the spatial derivatives of ∇ using, e.g., Diamond-Difference method (43) will result in a set of coupled linear equations. These equations can be solved via iterative approaches (44). Radiation dose will be computed using a discretized version of Eq. [6], once ψg,d(x) is available.

Numerically solving the BTE on a GPU could be extremely efficient. Not only are the matrix-vector operations within a BTE solver particularly favored by the GPU’s SIMD processing scheme, it also avoids the memory conflict issue encountered in GPU-based MC simulations. This method combines the accuracy advantage of a MC method and avoids its limitations. Hence, it is very promising to develop a dose calculation engine via this approach with clinically desired features. Further investigations along this road are currently in progress.

Discussion and conclusions

In this paper, we have reviewed a set of currently available GPU-based dose calculation algorithms for proton therapy. For pencil-beam type algorithms, although an extremely high efficiency can be achieved on GPU, the unsatisfactory accuracy, especially in some complicated clinical cases, becomes a significant concern. With the continuous growth of computational power and developments of new algorithms, the pencil-beam algorithms may be gradually replaced. Among those MC simulation methods, the full MC one attains a well guaranteed accuracy, while its efficiency is limited to a certain extent due to the inherent conflict between the GPU SIMD structure and the MC randomness, as well as the memory writing conflict issue. On the other hand, even though the simplified MC or the track-repeating MC reduces the computational weight significantly, the gain in terms of absolute computation time is not particularly attractive (not to mention the potential degradation of precision). Finally, a new dose calculation method via solving the Boltzmann transport equation is presented. With all the relevant physics included in this model and the underlying matrix-vector operations in the numerical computation that are suitable for GPU parallel processing, it is promising for this method to achieve a combined accuracy and efficiency.

Despite the achieved efficiency so far, a few research directions could also be explored in near future to further accelerate proton dose calculations. These efforts will contribute significantly towards realizing some advanced proton therapy treatment techniques that are currently limited by the computational speed. From the hardware point of view, it is always possible to keep enhancing the efficiency with faster GPUs. For example, the recently available next generation NVIDIA GPUs in the Kepler family delivers almost three times higher peak processing powers than previous GPUs. Moreover, if a multi-GPU platform is available, many of the aforementioned methods can be further parallelized among GPUs. Especially for MC simulations, all the particle histories can be simply distributed among GPUs, which then execute simultaneously without interfering with each other. Due to the negligible overhead in this process, it is expected that a roughly linear scalability of the computation efficiency can be achieved with respect to the number of GPUs. In a recently work, it has been reported that this linear scalability holds at least on a quad-GPU system (16). Another direction worth exploring is to develop new algorithms. Algorithm-based acceleration is usually much more efficient in terms of boosting processing speed than hardware based acceleration. Nonetheless, the intellectual difficulty is large and will require a series of novel inventions. Especially in the GPU context; it is an interesting, difficult, and important research topic to design GPU-suitable algorithms.

In retrospect, GPU has been applied for proton dose calculations for only a few years. The tremendous achievements to date have already opened a new door to allow much advanced dose calculation techniques. It is reasonable to believe that with continuous efforts on this research topic more and more developments will soon become available that will inevitably contribute to this field and benefit patients under proton therapy treatments.

Acknowledgments

Funding: This work is supported in part by the University of California Lab Fees Research Program.

Footnote

Provenance and Peer Review: This article was commissioned by the Guest Editors (Huan Giap and Eric Y Chuang) for the series “Particle Beam Therapy I” published in Translational Cancer Research. The article has undergone external peer review.

Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.3978/j.issn.2218-676X.2012.10.03). The series “Particle Beam Therapy I” was commissioned by the editorial office without any funding or sponsorship. KTM serves as an unpaid editorial board member of Translational Cancer Research. The authors have no other conflicts of interest to declare.

Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.

Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.

References

1. Miller DW. A review of proton beam radiation therapy. Med Phys 1995;22:1943-54. [PubMed]
2. Bonnett DE. Current developments in proton therapy: a review. Phys Med Biol 1993;38:1371-92. [PubMed]
3. Lomax AJ, Boehringer T, Coray A, et al. Intensity modulated proton therapy: a clinical example. Med Phys 2001;28:317-24. [PubMed]
4. Oelfke U, Bortfeld T. Inverse planning for photon and proton beams. Med Dosim 2001;26:113-24. [PubMed]
5. Paganetti H, Jiang H, Trofimov A. 4D Monte Carlo simulation of proton beam scanning: modelling of variations in time and space to study the interplay between scanning pattern and time-dependent patient geometry. Phys Med Biol 2005;50:983-90. [PubMed]
6. Kang Y, Zhang X, Chang JY, et al. 4D Proton treatment planning strategy for mobile lung tumors. Int J Radiat Oncol Biol Phys 2007;67:906-14. [PubMed]
7. Paganetti H, Jiang H, Parodi K, et al. Clinical implementation of full Monte Carlo dose calculation in proton beam therapy. Phys Med Biol 2008;53:4825-53. [PubMed]
8. Petti PL. Differential-pencil-beam dose calculations for charged particles. Med Phys 1992;19:137-49. [PubMed]
9. Lee M, Nahum AE, Webb S. An empirical method to build up a model of proton dose distribution for a radiotherapy treatment planning package. Phys Med Biol 1993;38:989-98.
10. Szymanowski H, Oelfke U. Two-dimensional pencil beam scaling: an improved proton dose algorithm for heterogeneous media. Phys Med Biol 2002;47:3313-30. [PubMed]
11. Gu X, Choi D, Men C, et al. GPU-based ultra-fast dose calculation using a finite size pencil beam model. Phys Med Biol 2009;54:6287-97. [PubMed]
12. Fujimoto R, Kurihara T, Nagamine Y. GPU-based fast pencil beam algorithm for proton therapy. Phys Med Biol 2011;56:1319-28. [PubMed]
13. Jacques R, Taylor R, Wong J, et al. Towards real-time radiation therapy: GPU accelerated superposition/convolution. Comput Methods Programs Biomed 2010;98:285-92. [PubMed]
14. Hissoiny S, Ozell B, Després P. Fast convolution-superposition dose calculation on graphics hardware. Med Phys 2009;36:1998-2005. [PubMed]
15. Jia X, Gu X, Sempau J, et al. Development of a GPU-based Monte Carlo dose calculation code for coupled electron-photon transport. Phys Med Biol 2010;55:3077-86. [PubMed]
16. Jia X, Gu X, Graves YJ, et al. GPU-based fast Monte Carlo simulation for radiotherapy dose calculation. Phys Med Biol 2011;56:7017-31. [PubMed]
17. Hissoiny S, Ozell B, Bouchard H, et al. GPUMCD: A new GPU-oriented Monte Carlo dose calculation platform. Med Phys 2011;38:754-64. [PubMed]
18. Yepes PP, Mirkovic D, Taddei PJ. A GPU implementation of a track-repeating algorithm for proton radiotherapy dose calculations. Phys Med Biol 2010;55:7107-20. [PubMed]
19. Kohno R, Hotta K, Nishioka S, et al. Clinical implementation of a GPU-based simplified Monte Carlo method for a treatment planning system of proton beam therapy. Phys Med Biol 2011;56:N287-94.
20. Jia X, Schümann J, Paganetti H, et al. GPU-based fast Monte Carlo dose calculation for proton therapy. Phys Med Biol 2012;57:7783-97. [PubMed]
21. Badal A, Badano A. Accelerating Monte Carlo simulations of photon transport in a voxelized geometry using a massively parallel graphics processing unit. Med Phys 2009;36:4878-80. [PubMed]
22. Jia X, Yan H, Gu X, et al. Fast Monte Carlo simulation for patient-specific CT/CBCT imaging dose calculation. Phys Med Biol 2012;57:577-90. [PubMed]
23. NVIDIA. NVIDIA CUDA Compute Unified Device Architecture, Programming Guide 2011,4.0.
24. Schaffner B, Pedroni E, Lomax A. Dose calculation models for proton treatment planning using a dynamic beam delivery system: an attempt to include density heterogeneity effects in the analytical dose calculation. Phys Med Biol 1999;44:27-41. [PubMed]
25. Paganetti H. Range uncertainties in proton therapy and the role of Monte Carlo simulations. Phys Med Biol 2012;57:R99-117. [PubMed]
26. Li JS, Shahine B, Fourkal E, et al. A particle track-repeating algorithm for proton beam dose calculation. Phys Med Biol 2005;50:1001-10. [PubMed]
27. Kohno R, Takada Y, Sakae T, et al. Experimental evaluation of validity of simplified Monte Carlo method in proton dose calculations. Phys Med Biol 2003;48:1277-88. [PubMed]
28. Yepes P, Randeniya S, Taddei PJ, et al. Monte Carlo fast dose calculator for proton radiotherapy: application to a voxelized geometry representing a patient with prostate cancer. Phys Med Biol 2009;54:N21-8.
29. Fippel M, Soukup M. A Monte Carlo dose calculation algorithm for proton therapy. Med Phys 2004;31:2263-73. [PubMed]
30. Chen GT, Singh RP, Castro JR, et al. Treatment planning for heavy ion radiotherapy. Int J Radiat Oncol Biol Phys 1979;5:1809-19. [PubMed]
31. Highland V. Some practical remarks on multiple scattering. Nuclear Instruments & Methods 1975;129:497-9.
32. Agostinelli S, Allison J, Amako K, et al. GEANT4-a simulation toolkit. Nuclear Instruments & Methods 2003;506:250-303.
33. Pratx G, Xing L. GPU computing in medical physics: a review. Med Phys 2011;38:2685-97. [PubMed]
34. Perl J, Shin J, Schumann J, et al. TOPAS: an innovative proton Monte Carlo platform for research and clinical applications. Med Phys 2012;39:6818-37. [PubMed]
35. Gifford KA, Horton JL, Wareing TA, et al. Comparison of a finite-element multigroup discrete-ordinates code with Monte Carlo for radiotherapy calculations. Phys Med Biol 2006;51:2253-65. [PubMed]
36. Lewis HW. Multiple scattering in an infinite medium. Phys Rev 1950;78:526-9.
37. Börgers C. Complexity of Monte Carlo and deterministic dose-calculation methods. Phys Med Biol 1998;43:517-28. [PubMed]
38. Fogliata A, Nicolini G, Clivio A, et al. Accuracy of Acuros XB and AAA dose calculation for small fields with reference to RapidArc(®) stereotactic treatments. Med Phys 2011;38:6228-37. [PubMed]
39. Zourari K, Pantelis E, Moutsatsos A, et al. Dosimetric accuracy of a deterministic radiation transport based 192Ir brachytherapy treatment planning system. Part I: single sources and bounded homogeneous geometries. Med Phys 2010;37:649-61. [PubMed]
40. Vassiliev ON, Wareing TA, Davis IM, et al. Feasibility of a multigroup deterministic solution method for three-dimensional radiotherapy dose calculations. Int J Radiat Oncol Biol Phys 2008;72:220-7. [PubMed]
41. Luo Z. An overview of the bipartition model for charged particle transport. Radiation Physics and Chemistry 1998;53:305-27.
42. Luo ZM, Brahme A. An overview of the transport theroy of charged particles. Radiation Physics and Chemistry 1993;41:673-703.
43. Lewis EE, Miller WF. eds. Computational Methods of Neutron Transport. New York: Wiley, John & Sons, 1984.
44. Golub GH, van Loan CF. eds. Matrix computation. Baltimore: Johns Hopkins University Press, 1996.