A LASSO-based survival prediction model for patients with synchronous colorectal carcinomas based on SEER

Introduction

Colorectal cancer (CRC) is the third common cancer and ranks third as a cause of cancer-related death for males in America (1,2). The definition of multiple primary colorectal carcinomas (MPCC) is the presence of 2 or more primary invasive adenocarcinomas diagnosed in patients. Synchronous colorectal carcinomas (SCC) is identified as the second invasive adenocarcinomas diagnosis within 6 months after the first invasive adenocarcinomas diagnosis (3). Metachronous colorectal carcinomas (MCC) is identified as the second invasive adenocarcinomas diagnosis after more than 6 months after the first invasive adenocarcinomas diagnosis (4). Among patients suffering from CRC, SCC contribute 1% to 8% (5). Patients with SCC must be fully studied since it’s not a rare incident of SCC among CRC (6).

Currently, the literature of SCC is mostly small series (<80 patients) which described epidemiology and clinicopathology (3-5,7-9). In these studies, a part of them indicated there was no appreciable differences between patients with synchronous tumors and single neoplasm in survival when compared to individuals who had single neoplasms. In contrast, the other part of them indicated individuals who had metachronous carcinomas have been observed to show a poor clinical outcome after the development of the second carcinoma (7). The prognosis of SCC still controversial. What’s more, there are few reports on the impact factors of synchronous colorectal carcinoma’s overall survival (OS) and formulation of prognostic models (8). So, we evaluated the impact factors of SCC on the OS and made a prognostic model with a large cohort of patients.

In this study, our aim was to develop and validate a nomogram based on treatment variables, surgical variables, clinical characteristics and tumor characteristics to predict the survival of SCC patients. The data was obtained from the population-based Surveillance, Epidemiology, and End Results (SEER) database which contains a large sample size and has a long follow-up time. Since the prediction model is associated with the first and second-time treatment variables, surgical variables and tumor characteristics, it may exist a multicollinearity problem between first and second-time variables. Furthermore, because of incorporating too many variables, there may be over-fitting in predicting model. For these reasons, we selected the least absolute shrinkage and selection operator (LASSO) method to deal with the above concerns. In order to determine whether the prediction model fitted with LASSO-based Cox regression was better, we compared the LASSO model (fit by Cox regression after variables selection by LASSO Cox regression) to the COX model (fit by Cox regression), TNM model (established in first time T, N, M grade) and TTNNMM model (established in first and second times T, N, M grade). We present the following article in accordance with the STROBE reporting checklist (available at https://tcr.amegroups.com/article/view/10.21037/tcr-20-1860/rc).

Methods

Data source

We identified the survivors from the National Cancer Institute’s Surveillance, Epidemiology, and End Results (SEER) 13-registry database by analyzing patients diagnosed from 2004 to 2013. The SEER has developed and maintained high-quality, validated data on causes of death among cancer survivors, providing insight into relative and cause-specific deaths in this population (10,11). Data was retrieved using SEER*Stat 8.3.5 (Surveillance Research Program, National Cancer Institute, Bethesda, MD). Our study was determined and it exempted the data from Colorectal Surgery Union Hospital in Fujian. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013).

Patients

Patients over 18 years old who were diagnosed with colorectal carcinoma between 2004 and 2013 with surgery were initially analyzed. Patients diagnosed with single colorectal carcinoma were excluded to explore SCC. Patients who survival time was unknown were excluded to explore the epidemiology, pathogenesis and factors that influenced the survival of SCC. Patients with an unknown grade of the tumor, unknown T stage, unknown N stage, and unknown M stage were excluded for further comparison of the feasibility of the TNM model and TTNNMM model. Patients with unknown prognostic characteristics (including race, tumor size and location) were also excluded. The clinicopathologic variables were then collected from the SEER 13 database, including gender, race, sex, delta t, months survived and first and second times age of diagnosis, marital, location of tumor, TNM staging (12), histologic grade, number of lymph nodes examined, number of positive lymph nodes, tumor size, radiation sequence, chemotherapy, and surgical related variables. Then, patients who had CRC more than 3 times or multiple metachronous primary carcinomas were excluded. Lastly, we excluded patients who survived less than 1 month or other variable unknown (Figure 1).

Figure 1 Flowchart of patient selection for this study. MPCC, multiple primary colorectal carcinomas.

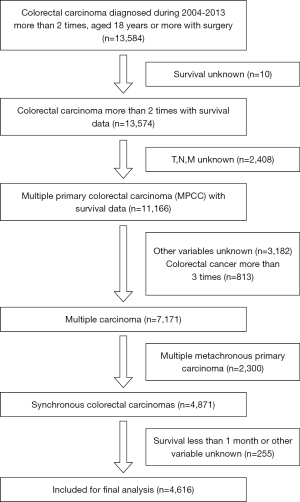
In the construction of the survival predicting model, the internal cohort included patients from SEER database, while the external validation cohort consisted of patients from Colorectal Surgery Union Hospital in Fujian database.

Statistical analysis

Statistical analysis was carried out with R software (version 3.4.2; http://www.Rproject.org) and SPSS (Statistical Product and Service Solutions, version 22.0). The packages in R used in this study are as follows. Statistical significance levels were all two-sided, with statistical significance set at 0.05.

Variables selection and models constructing

The LASSO method, which is suitable for the regression of high-dimensional data (13,14), was used to select the most useful predictive variables from the primary data set. The “glmnet” package was used to perform the LASSO Cox regression model analysis (15). To compare the differences in the Cox method and LASSO-based Cox method, we separately used the Cox regression or LASSO-based Cox regression to construct models. The COX model was selected and constructed using the internal cohort by backward Cox analysis using Akaike information criterion (AIC) selection criteria and the best model was selected with the least AIC (16-18). The LASSO model was selected and constructed using the internal cohort by LASSO-based Cox regression. The TNM model was established using the internal cohort by the first time T, N and M staging and that of TTNNMM model was established using the internal cohort by the first and second times T, N and M staging (19).

Compare models

The LASSO model using LASSO-based Cox regression and COX model using backward Cox analysis was first internally validated in the internal cohort using a bootstrap method (1,000 bootstraps resamples) and then externally validated in the external cohorts. The 3- and 5-year OS calibration of the LASSO model and COX model were performed by comparing the observed survival with the predicted survival in the internal and external cohorts. Then for survival testing with the LASSO model and COX model of the specificity, time-dependent receiver operating characteristic (timeROC) curves were estimated for two cohorts by inverse probability of censoring weighting estimators (KM-weight) at 3-, and 5-year (20,21). Sequential AUCs were compared among the four models using identically and independently distributed representations of the AUC estimators (22). Also, the overall prognostic performance of the four models was assessed using the Bayesian information criterion (BIC) via bootstrap-resampling analysis. Lastly, four models were evaluated with AIC, C-index (23), the net reclassification improvement (NRI) (24,25) and integrated discrimination improvement (IDI) (26).

Clinical use

The net benefit and clinical usefulness of the four models above were estimated with decision curve analysis (DCA) throughout the whole cohort (27).

Nomogram for a visualization model

For the purpose of illustration and clinical applicability, we created a nomogram based on the LASSO model. In the nomogram, model-based score points for each predictor variable category were displayed, which has to be summarized for any individual patient. From the resulting total number of points, the corresponding predicted survival probabilities from the nomogram could be easily read.

Results

Clinical characteristics

From the data obtained from 2004 to 2013, 4,616 patients with SCC in the SEER database were found. Patient characteristics are shown in Table 1. There are significant correlations in age and slight correlation in pN, pM, examined lymph nodes, Surg Prim Site, and chemotherapy between the twice synchronous colorectal. Patients with SCC were mostly older (>65 years), more often men (54.1%), and likely to have a depth of invasion by T3 (56.8% and 41.5% by the first and second times). Tumors were mostly situated in the cecum, ascending colon and sigmoid colon.

Predictive variable selection

It was showed that 31 variables were reduced to 11 potential predictors on the basis of 4,616 patients by LASSO-based Cox regression in the internal cohort (Figure 2A-2C) or were reduced to 16 potential predictors by Cox regression base minute AIC (Figure 2D).

Figure 2 The LASSO Cox regression model was used to select predicted variables. (A) Tuning parameter (λ) selection in the LASSO model used 10-fold cross-validation via minimum criteria. The partial likelihood deviance curve was plotted versus log (λ). Dotted vertical lines were drawn at the optimal values using the minimum criteria and the 1 standard error of the minimum criteria (the 1-SE criteria). A λ value of 0.034, with log (λ), −3.385 was chosen (1-SE criteria) according to 10-fold cross-validation. (B) LASSO coefficient profiles of the 31 variables. A coefficient profile plot was produced against the log (λ) sequence. The vertical line was drawn at the value selected using 10-fold cross-validation, where optimal λ resulted in 11 nonzero coefficients. Multivariable analysis of factors affecting OS by Cox regression and LASSO combine Cox regression. (C) The plot shows the HRs (squares) and 95% CIs (lines) of LASSO combine multivariable Cox regression. (D) The plot shows the HRs (squares) and 95% CIs (lines) of multivariable Cox regression. The figure shows all of the significant covariates. The vertical line represents an HR of 1 for reference. LASSO, least absolute shrinkage and selection operator; OS, overall survival; HR, hazard ratio.

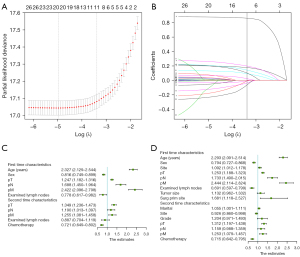
Results of the selected variables with Cox regression and LASSO-based Cox regression are listed in Table 2. Table 2 indicates that the age of the first time SCC diagnosis, sex, first time size, first time surgery, second time marital, second time grade, second time chemotherapy, first and second times pT, pN, pM, regional nodes examined and site of disease was significantly associated with OS by Cox regression. Table 2 also indicates that the age of first time SCC diagnosis, sex, second-time chemotherapy, first and second times pT, pN, pM, regional nodes examined were significantly associated with OS by LASSO-based Cox regression.

Results from the relation between first and second times pT, pN, pM, grade and regional nodes are listed in Table 1.

Development of COX model and LASSO model

The multivariable regression model for age, sex, marital, race, site, pT, pN, pM, radiation, chemotherapy, surgery, nodes examined, etc. were included in the regression after variables were selected by the LASSO-based Cox regression or Cox regression. We showed hazard ratios with 95% CIs for covariates which are included in Table 2.

Apparent performance of the LASSO model or COX model in the internal cohort

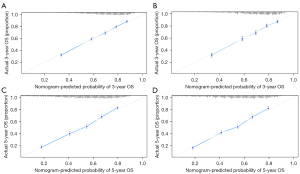
The calibration curves of the LASSO model and COX model for the probability of OS in 3- and 5-year between prediction and observation in the internal cohort (Figure 3A-3D) were plotted to assess the calibration of the COX model and LASSO model, which were accompanied with the Hosmer-Lemeshow test (A significant test statistic implies that the model calibrates perfectly).

Figure 3 Calibration curves of the Cox nomogram and the LASSO model in each cohort. (A) Calibration curve of 3-years OS of the Cox model in the primary cohort. (B) Calibration curve of 3-year OS of the LASSO nomogram in the primary cohort. (C) Calibration curve of 5-year OS of the Cox model in the primary cohort. (D) Calibration curve of 5-year OS of the LASSO nomogram in the primary cohort. The y-axis represents the actual OS. Calibration curves depict the calibration of each model in terms of the agreement between the predicted risks of predicted OS and actual OS. The y-axis represents the actual OS. The x-axis represents the predicted OS. The diagonal dotted line represents a perfect prediction by an ideal model. The blue solid line represents the performance of the model, of which a closer fit to the diagonal dotted line represents a better prediction. LASSO, least absolute shrinkage and selection operator; OS, overall survival.

Validation of the LASSO model and COX model

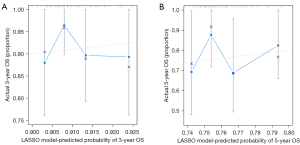
The external validation was tested in the external cohort. The LASSO model was formed in the internal cohort and was applied to all the patients of the external cohort. The calibration curves in 3- and 5-year (Figure 4A,4B) were derived on the basis of the regression analysis.

Figure 4 Calibration curve of the LASSO model in the validation cohort. (A) Calibration curve of 3-year OS of the LASSO model in the validation cohort. (B) Calibration curve of 5-year OS of the LASSO model in the validation cohort. OS, overall survival; LASSO, least absolute shrinkage and selection operator.

C-index and AIC

To quantify the discrimination performance of the LASSO model, COX model, TNM model, and TTNNMM model, Harrell’s C-index and AIC were applied (Table 3). The C-index for the LASSO model, COX model, TNM model and TTNNMM model were 0.710 (95% CI: 0.703 to 0.717), 0.712 (95% CI: 0.705 to 0.719), 0.637 (95% CI: 0.631 to 0.644) and 0.651 (95% CI: 0.644 to 0.657), which were confirmed to be 0.710, 0.712, 0.637 and 0.651 via bootstrapping validation. The AIC for the LASSO model, COX model, TNM model, and TTNNMM model were 33,431, 33,420, 34,043, 33,994. According to C-index and AIC, there are no significant difference between COX model and LASSO model.

Predictive accuracy of COX model and LASSO model

According to the survROC curves for 1-, 3-, 5-year OS for LASSO model, the COX model, TNM model, and TTNNMM model (Figure 5A-5D), the ROC curve (a general measure of predictiveness) was found to be greater in 3- and 5-year.

Figure 5 ROC curve of the prognosis of patients at 1, 3 and 5-year point in the 2004–2013 primary cohort. (A) ROC curve of the LASSO model in prediction of prognosis of patients at 1, 3 and 5-year point in the 2004–2013 primary cohort. (B) ROC curve of the COX model in prediction of prognosis of patients at 1, 3 and 5-year point in the 2004–2013 primary cohort. (C) ROC curve of the TNM stage model in prediction of prognosis of patients at 1, 3 and 5-year point in the 2004–2013 primary cohort. (D) ROC curve of the TTNNMM stage model in prediction of prognosis of patients at 1, 3 and 5-year point in the 2004–2013 primary cohort. ROC, receiver operating characteristic; LASSO, least absolute shrinkage and selection operator.

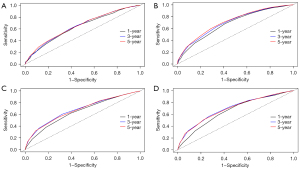
Whether apparent different performance of the LASSO and COX model

TimeAUC

Time-dependent ROC curves were generated to compare the sequential trends of the LASSO, COX, TNM and TTNNMM model for OS. The time-dependent ROC curve of the LASSO model was continuously superior to that of the COX model, TNM model and TTNNMM model (Figure 6).

Figure 6 Time-dependent ROC curves for the LASSO, COX, TNM, and TTNNMM model. The horizontal axis represents year after diagnosis and the vertical axis represents the estimated area under the ROC curve for survival at the time of interest. Blue, red, black and gray solid lines represent the estimated AUCs of the LASSO, COX, TNM and TTNNMM model. LASSO model: the model fit by Cox regression after variables selection by LASSO Cox regression; COX model: the model fit by Cox regression; TNM model: the model established in first time T, N, M grade; TTNNMM model: the model established in first and second times T, N, M grade. ROC, receiver operating characteristic; LASSO, least absolute shrinkage and selection operator.

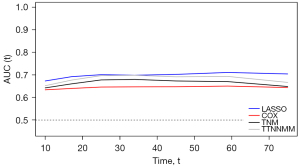
BIC

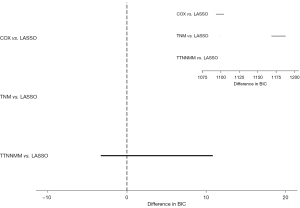
The prognostic performances of the LASSO, COX, TNM, and TTNNMM model were compared using BIC, which is not only a measure of the goodness of fit of an estimated statistical model but also accurately considers the number of parameters included in the model. As shown in Figure 7, there was no significant difference between the COX and LASSO model after the bootstrap analysis (BIC 4.49, 95% CI: –2.92 to 11.91) but there was a significant difference between the TNM and LASSO model (BIC 1,178.76, 95% CI: 1,171.15–1,186.37), also TTNNMM and LASSO model (BIC 1,098.57, 95% CI: 1,092.05–1,105.09).

Figure 7 Results of the BIC level of the 4 different models. By the BIC via bootstrap analysis (1,000 samples, 95% CI limits are shown). BIC, Bayesian information criterion.

NRI and IDI

The discriminant ability for LASSO model, COX model, TNM model, and TTNNMM model was calculated using NRI and IDI (Table 4). Compared to the TNM model and TTNNMM model, LASSO model was found to be a higher discriminant and possess reclassification indices (IDI 0.072 and 0.064; P<0.001; NRI 0.525 and 0.466) (Table 4). In addition, compared to the COX model, the LASSO model doesn’t significantly decrease the discriminant and reclassification indices (IDI −0.002, P=0.058; NRI −0.009) (Table 4).

Clinical use

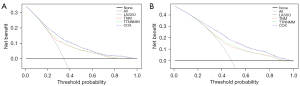
DCA was conducted to determine the clinical usefulness of the LASSO model by quantifying the net benefits at different threshold probabilities. We also plotted the decision curve for the four models in 3- and 5-year (Figure 8A,8B).

Figure 8 Decision curve analysis for the TNM model, TTNNMM model, Cox model and LASSO model in the prediction of prognosis of patients at 3- and 5-year point. The y-axis measures the net benefit. The black dotted line represents the LASSO model. The blue dotted line represents the COX model. The green dotted line represents the TTNNMM model. The red dotted line represents the TNM model. The black line represents the assumption that no patients died. The grey line represents the assumption that all patients died. The net benefit was calculated by subtracting the proportion of all patients who are false positive from the proportion who are truly positive, weighting by the relative harm of forgoing treatment compared with the negative consequences of unnecessary treatment. The decision curve showed that if the threshold probability of a patient or doctor is >5%, using the LASSO model in the current study to predict OS more benefit than the treat-all-patients scheme or the treat-none scheme. The net benefit was not comparable, with several overlaps, on the basis of the LASSO model and the COX model. LASSO, least absolute shrinkage and selection operator; OS, overall survival.

Visualization of SCC survival prediction model

Survival prediction model of the nomogram was established based on factors selected by LASSO-based Cox regression (Figure 9). The nomogram showed that first time age had the most contribution to prognosis, followed by first- and second-times T stage, N stage, metastases and examined lymph nodes. Sex had a modest effect on survival. Each subtype of the variables was assigned a score. A straight line can be drawn down at each time point on the total point scale to determine the estimated probability of survival, according to the total number of points. For each predictor, the points assigned on the 0–10 scale at the top are read and then these points are added. The number on the “Total Points” scale were found and then the corresponding predictions of 3-, and 5-year risk are recorded.

Figure 9 Developed LASSO model nomogram. The LASSO model nomogram was developed in the primary cohort, with the first time age and sex, the second time chemotherapy and the first and second times pT, pN, pM, and regional nodes examined incorporated. LASSO model nomograms to predict 3- and 5-year overall survival probability with SCC. For each predictor, read the points assigned on the 0–10 scale at the top and then add these points. Find the number on the “Total Points” scale and then read the corresponding predictions of 3- and 5-year risk. LASSO, least absolute shrinkage and selection operator; SCC, synchronous colorectal carcinomas.

Discussion

In this study, we developed and validated a prognostic model about SCC which based on large data from SEER by LASSO-based Cox regression. Our results show that the OS is associated with age, sex, second-time chemotherapy and first and second times pT, pN, pM.

Notably, the second time examined lymph nodes didn’t show enough predictive strength on the basis of Cox regression, which makes a common strategy to exclude this variable for model development. However, it may be a result of nuances in the data set or confounding by other predictors that reject important predictors (17,28), for which no significant statistical association with OS does not definitively imply that examined lymph nodes are unimportant. In addition, more lymph nodes examined may mean a better quality of operation. Therefore, we kept the second time examined lymph nodes as a candidate factor in the process of model development. For the same reason, we kept the first-time tumor size and the second-time grade and pN in the COX model.

Grade, size, surgery and marital which may be multi-collinearity bias with pT, pN, pM, and age were not included in the LASSO model. Grade, size, surgery may be associated with TNM grading (12). Besides, the old aged were more likely to be widowed. Also, because of overfitting site was not included in the LASSO model.

From Table 1, we found that patients with SCC were generally older (>65 years), more often male, and likely with the depth of invasion of T3. There may be less estrogen to protect in male (29) and a high probability of microsatellite instability (MSI) in older patients (30). Besides, it may be as a result of tumor biologic characteristics with the depth of invasion by T3. Therefore, patients who are older (>65 years), men, and depth of invasion by T3 should closely monitor the postoperative enteroscopy for early detection of SCC.

Tables 3,4 and Figures 3-8 show that there was no significant difference between the LASSO model and COX model (NRI, IDI, c index, ROC, AIC, and BIC) but the LASSO model was obviously better than the TNM model and TTNNMM model (NRI, IDI, c index, AIC, ROC, and BIC). Compared to the COX model, the LASSO model significantly reduced the variables included which minimized overfitting and collinearity. Moreover, Figure 6 shows that the LASSO model performs better than the Cox model in the timeAUC. Although the LASSO model included fewer variables, the LASSO model performed better in the timeAUC compared to the COX model.

The most important and final argument for the use of the nomogram is based on the need to interpret the individual need for additional treatment or care. However, the clinical consequences of a particular level of discrimination or degree of miscalibration cannot be adequately assessed by the risk-prediction discrimination, performance, and calibration (17,31). Therefore, in order to justify the clinical usefulness, it is crucial to ascertain whether the LASSO model-assisted decisions can improve patient outcomes. With this aim, in this study, the application of the DCA instead of the multi-institutional prospective for the validation of the model was performed. This novel method offers an insight into the clinical consequences on the basis of threshold probability, from which the net benefit could be derived (17,32). Through the decision curve plot, we can ascertain whether the probability of threshold of a patient or doctor is 5% using the LASSO model is more beneficial than either the TNM model or TTNNMM model and not inferior compared to the COX model (Figure 8A,8B).

There are some limitations in the present work that should be discussed. The collection of the SEER database is retrospective. There is a lack of molecular data and data for biological prognostic factors that might also influence the prognosis of SCC patients. In recent years, increased research with gene markers, such as MSI, SSA, BRAF V600E associated with SCC has been proposed (3,8). Moreover, there might be some increase in the bias that we excluded all patients who had missing data from the collected variables. The study didn’t incorporate detailed chemotherapy and radiation methods due to the lack of adequate information and large bias of the information. Finally, although this nomogram performed well in both internal and external cohorts, due to the influence of deaths related to the operation, the data should be used with caution when predicting 1-year risk. Even so, although it didn’t include the genomic characteristics, excluded patients who had missing data and was retrospect to analysis, it was the first model to perform a prognosis OS of SCC.

Based on the database content, the main influencing factors were screened for the LASSO model. Due to the limitations of the database, some important factors weren’t covered. In the future, we hope to have relevant data to incorporate it into our research.

In conclusion, this study presents a prognosis nomogram that incorporates both the first-time and the second-time variables and can be conveniently used to facilitate the prediction of OS in patients with SCC.

Acknowledgments

We thank all the staff in the Department of Colorectal Surgery of FMUUH and Dr. Jerry for polishing the manuscript.

Funding: This study was supported by National Clinical Key Specialty Construction Project (General Surgery) of China and Wu Jieping Medical Foundation (No. 320.2710.1833).

Footnote

Reporting Checklist: The authors have completed the STROBE reporting checklist. Available at https://tcr.amegroups.com/article/view/10.21037/tcr-20-1860/rc

Peer Review File: Available at https://tcr.amegroups.com/article/view/10.21037/tcr-20-1860/prf

Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://tcr.amegroups.com/article/view/10.21037/tcr-20-1860/coif). The authors have no conflicts of interest to declare.

Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013).

Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.

References

1. Siegel RL, Miller KD, Jemal A. Cancer statistics, 2018. CA Cancer J Clin 2018;68:7-30. [Crossref] [PubMed]
2. Huang YQ, Liang CH, He L, et al. Development and Validation of a Radiomics Nomogram for Preoperative Prediction of Lymph Node Metastasis in Colorectal Cancer. J Clin Oncol 2016;34:2157-64. [Crossref] [PubMed]
3. Hu H, Chang DT, Nikiforova MN, et al. Clinicopathologic features of synchronous colorectal carcinoma: A distinct subset arising from multiple sessile serrated adenomas and associated with high levels of microsatellite instability and favorable prognosis. Am J Surg Pathol 2013;37:1660-70. [Crossref] [PubMed]
4. Brandariz L, Alegre C, Rueda D, et al. New Perspectives in Multiple Primary Colorectal Cancer: A Surgical Approach. Digestion 2016;94:57-65. [Crossref] [PubMed]
5. van Leersum NJ, Aalbers AG, Snijders HS, et al. Synchronous colorectal carcinoma: a risk factor in colorectal cancer surgery. Dis Colon Rectum 2014;57:460-6. [Crossref] [PubMed]
6. Papadopoulos V, Michalopoulos A, Basdanis G, et al. Synchronous and metachronous colorectal carcinoma. Tech Coloproctol 2004;8:s97-s100. [Crossref] [PubMed]
7. Fante R, Roncucci L, Di Gregorio C, et al. Frequency and clinical features of multiple tumors of the large bowel in the general population and in patients with hereditary colorectal carcinoma. Cancer 1996;77:2013-21. [Crossref] [PubMed]
8. Lam AK, Chan SS, Leung M. Synchronous colorectal cancer: clinical, pathological and molecular implications. World J Gastroenterol 2014;20:6815-20. [Crossref] [PubMed]
9. Liu YL, Xu HT, Jiang SX, et al. Prognostic significance of lymph node status in patients with metastatic colorectal carcinoma treated with lymphadenectomy. J Surg Oncol 2014;109:234-8. [Crossref] [PubMed]
10. Howlader N, Ries LA, Mariotto AB, et al. Improved estimates of cancer-specific survival rates from population-based data. J Natl Cancer Inst 2010;102:1584-98. [Crossref] [PubMed]
11. Mariotto AB, Noone AM, Howlader N, et al. Cancer survival: an overview of measures, uses, and interpretation. J Natl Cancer Inst Monogr 2014;2014:145-86. [Crossref] [PubMed]
12. Amin MB, Greene FL, Edge SB, et al. The Eighth Edition AJCC Cancer Staging Manual: Continuing to build a bridge from a population-based to a more "personalized" approach to cancer staging. CA Cancer J Clin 2017;67:93-9.
13. Sauerbrei W, Royston P, Binder H. Selection of important variables and determination of functional form for continuous predictors in multivariable model building. Stat Med 2007;26:5512-28. [Crossref] [PubMed]
14. Tibshirani R. Regression shrinkage and selection via the lasso: A retrospective. J R Statist Soc B 2011;73:273-82. [Crossref]
15. Tibshirani R. The lasso method for variable selection in the Cox model. Stat Med 1997;16:385-95. [Crossref] [PubMed]
16. Venables WN, Ripley BD. Modern Applied Statistics with S. Statistics & Computing 2002;52:704-5.
17. Collins GS, Reitsma JB, Altman DG, et al. Transparent Reporting of a Multivariable Prediction Model for Individual Prognosis or Diagnosis (TRIPOD): the TRIPOD Statement, 2015.
18. Sauerbrei W, Boulesteix AL, Binder H. Stability investigations of multivariable regression models derived from low- and high-dimensional data. J Biopharm Stat 2011;21:1206-31. [Crossref] [PubMed]
19. Rao SJ. Regression Modeling Strategies: With Applications to Linear Models, Logistic Regression, and Survival Analysis by Frank E. Harrell. Publications of the American Statistical Association 2005;98:257-8. [Crossref]
20. Blanche P, Dartigues JF, Jacqmin-Gadda H. Estimating and comparing time-dependent areas under receiver operating characteristic curves for censored event times with competing risks. Stat Med 2013;32:5381-97. [Crossref] [PubMed]
21. Heagerty PJ, Lumley T, Pepe MS. Time-dependent ROC curves for censored survival data and a diagnostic marker. Biometrics 2000;56:337-44. [Crossref] [PubMed]
22. Rodríguez-Álvarez MX, Meira-Machado L, Abu-Assi E, et al. Nonparametric estimation of time-dependent ROC curves conditional on a continuous covariate. Stat Med 2016;35:1090-102. [Crossref] [PubMed]
23. Hanley JA, McNeil BJ. A method of comparing the areas under receiver operating characteristic curves derived from the same cases. Radiology 1983;148:839-43. [Crossref] [PubMed]
24. Pencina MJ, D'Agostino RB Sr, Steyerberg EW. Extensions of net reclassification improvement calculations to measure usefulness of new biomarkers. Stat Med 2011;30:11-21. [Crossref] [PubMed]
25. Tangri N, Stevens LA, Griffith J, et al. A predictive model for progression of chronic kidney disease to kidney failure. JAMA 2011;305:1553-9. [Crossref] [PubMed]
26. Chambless LE, Cummiskey CP, Cui G. Several methods to assess improvement in risk prediction models: extension to survival analysis. Stat Med 2011;30:22-38. [Crossref] [PubMed]
27. Vickers AJ, Cronin AM, Elkin EB, et al. Extensions to decision curve analysis, a novel method for evaluating diagnostic tests, prediction models and molecular markers. BMC Med Inform Decis Mak 2008;8:53. [Crossref] [PubMed]
28. Collins GS, Reitsma JB, Altman DG, et al. Transparent reporting of a multivariable prediction model for individual prognosis or diagnosis (TRIPOD): the TRIPOD Statement. Eur J Clin Invest 2015;45:204-14. [Crossref] [PubMed]
29. Fernandez E, La Vecchia C, Braga C, et al. Hormone replacement therapy and risk of colon and rectal cancer. Cancer Epidemiol Biomarkers Prev 1998;7:329-33. [PubMed]
30. Seo HM, Chang YS, Joo SH, et al. Clinicopathologic characteristics and outcomes of gastric cancers with the MSI-H phenotype. J Surg Oncol 2009;99:143-7. [Crossref] [PubMed]
31. Van Calster B, Vickers AJ. Calibration of risk prediction models: impact on decision-analytic performance. Med Decis Making 2015;35:162-9. [Crossref] [PubMed]
32. Balachandran VP, Gonen M, Smith JJ, et al. Nomograms in oncology: more than meets the eye. Lancet Oncol 2015;16:e173-80. [Crossref] [PubMed]